今天我们一起来学习下关于电容器的充电和放电的知识点：

把一个电容为C的电容器连接到电压为V0的电池充电时，电容器贮存的电荷Q会增加，最终达致Q=CV0；而电容器的电压（VC）也会随电荷累积而增加，最终达至VC=V0；虽然电容器本身不能导电，没有闭合电路，但由于刚连接时有电势差，所以会短暂产生电流，直至VC=V0，电流便无法再通过了。

我们可以把整个过程中，电容器的Q、V和电路的I随着时间的变化推导出来。

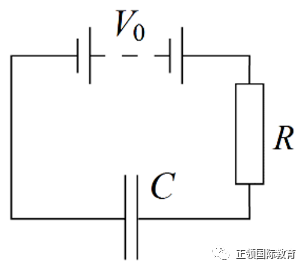
首先，整个电路的电势差为电池的电动势减去电容的电势差，这又等于电路的IR。所以

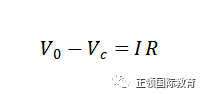
当电流I流通时，电容器的电荷Q便会增加，I等于电容器的Q随时间的变化率。

我们可以把整个过程中，电容器的Q、V和电路的I随着时间的变化推导出来。

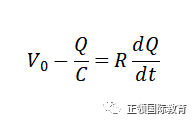
整理一下，然后进行积分。刚开始时（即t=0），电容器没有电荷，所以Q=0。经过时间t后，电容器电荷增至Q。所以t的范围由0至t，Q的范围由0至Q。可以得出Q随t变化的公式。

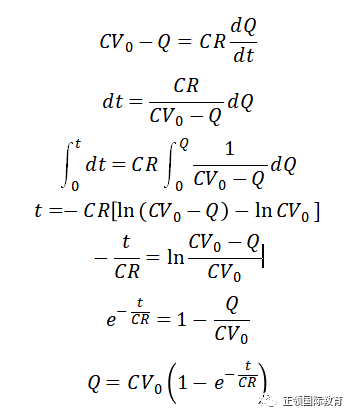
参看这公式，若t不断增大，Q便趋向CV0，即电容器能贮存的电量。

然后，因为Q=CV，可得出V随t变化的公式。

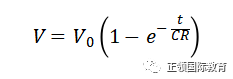
参看这公式，若t不断增大，V便趋向V0，即电容器会达致和电池同电压。

最后还有电流I，可以这样找：

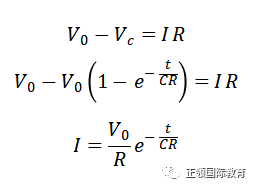
参看这公式，初始的I等于V0除以R，刚开始时电势差最大，导出最大的电流。但电流随时间会指数衰减，最终趋向0。

把三幅曲线图画出来，是这样的：

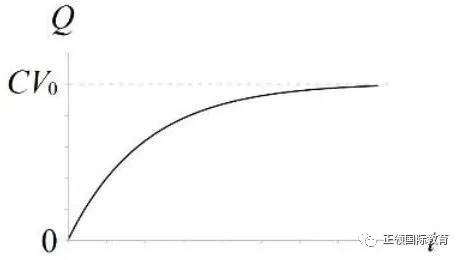
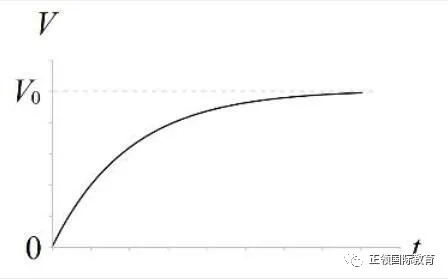
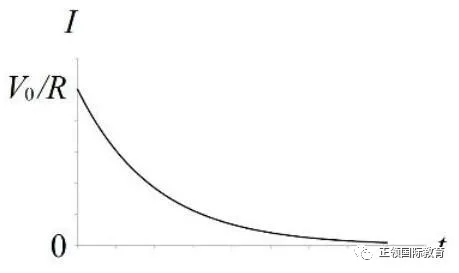
V和Q的形状相同，也是上升的曲线。I的形状像倒过来，是下降的曲线，而且是典型的指数衰减曲线。

对照指数衰减的函数，衰减常数k等于1/CR，而CR又称为时间常数。衰减常数愈大（或时间常数愈小），衰减愈快。所以可以说，若C和R的乘积愈大，衰减愈慢，需要愈长时间完成充电。

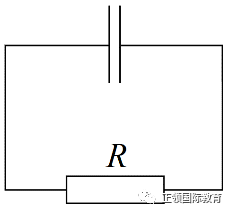
至于放电过程，把电容器连接至电阻器R上，电容器的电势差导出电流，所以：

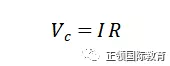
当电流流通的时候，电容内的电荷会减少，所以I等如负Q的时间变化率。

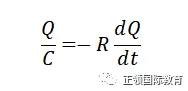
然后用积分，起初，电容器充满电荷，电量为CV0，经过时间t后，电量减少至Q，所以

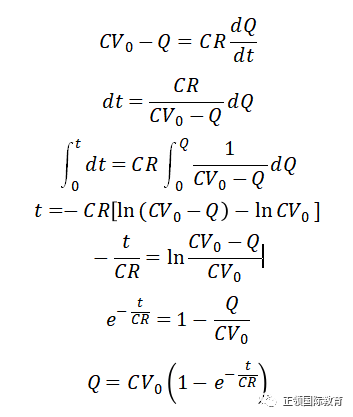
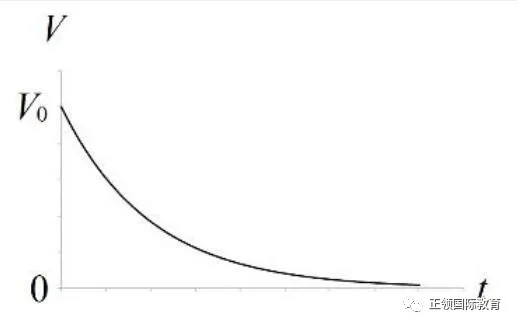
参看这公式，Q由最初的CV0，随时间指数衰减，最终趋向0。

然后，因为Q = CV，可得出V随t变化的公式。

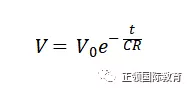
参看这公式，V由最初的V0，随时间指数衰减，最终趋向0。

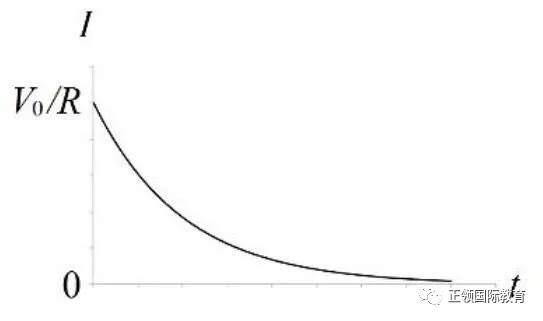
电流I可以V除以R得出：

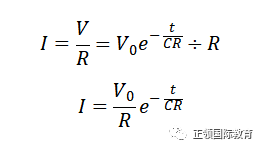
参看这公式，初始的I等于V0除以R，刚开始时电势差最大，导出最大的电流。但电流随时间会指数衰减，最终趋向0。

把三幅曲线图画出来，是这样的：

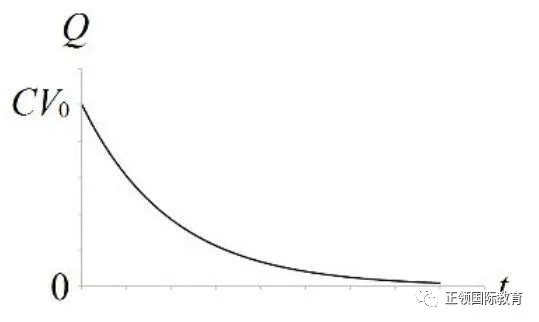
 好啦，今天的题目就讲解到这里，欢迎同学们留言互动探讨喔！