大家好,运动学的题型我们已经讲完了,以下是上次练习题的答案给小伙伴们参考。

今天我将为大家带来m1中力学部分的讲解和分析,这一章要讲的是牛二和平衡。虽然内容多且繁琐,但大家只需掌握核心知识点,即可逐题攻破。
首先复习一下牛顿第一定律和牛顿第二定律。
牛一:在没有外力作用下,物体保持静止或均速直线运动。它是一个平衡状态。
牛二:外力会改变物体的运动状态,即F=ma。它是一个非平衡状态。
当我们学过力的分解之后会知道,
平衡状态:两个方向的合力均为0.
非平衡状态:平行于运动方向的合力F=ma,垂直于运动方向的合力为0。
题型一:Force and motion 需要用到的是牛顿第二定律
问题1
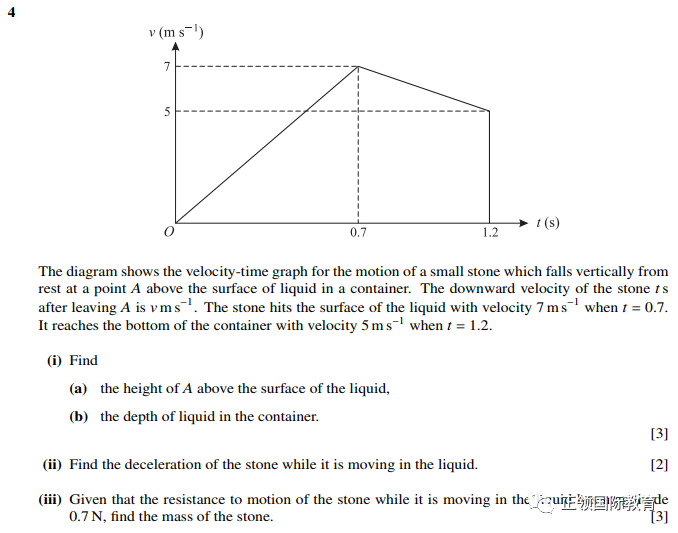
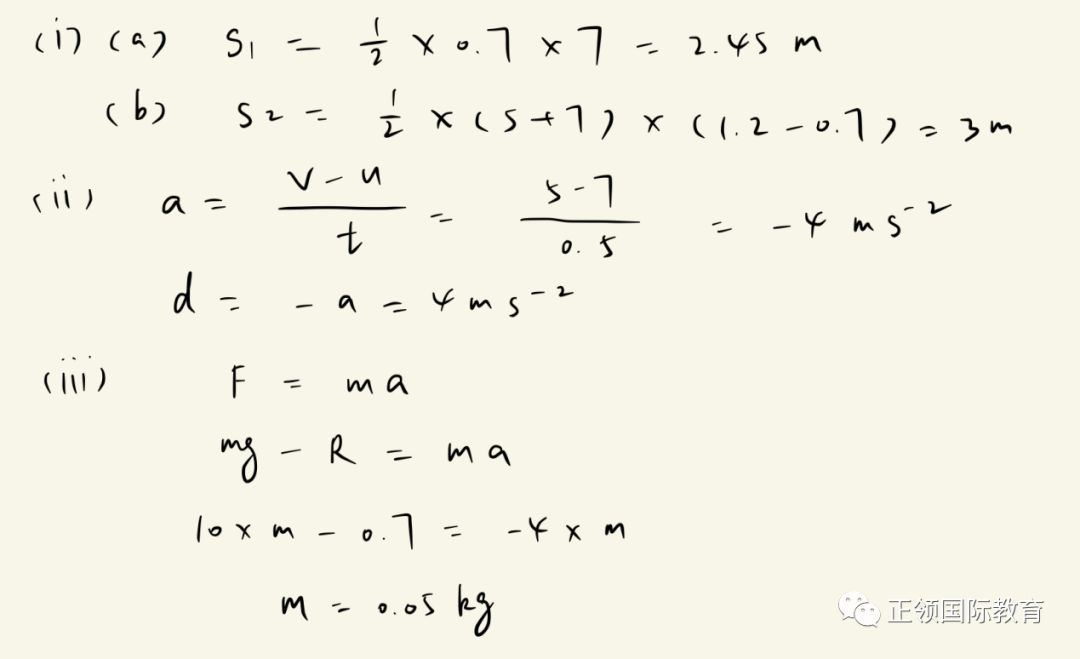
请注意在使用公式F=ma时,F为合外力。
题型二:力的分解
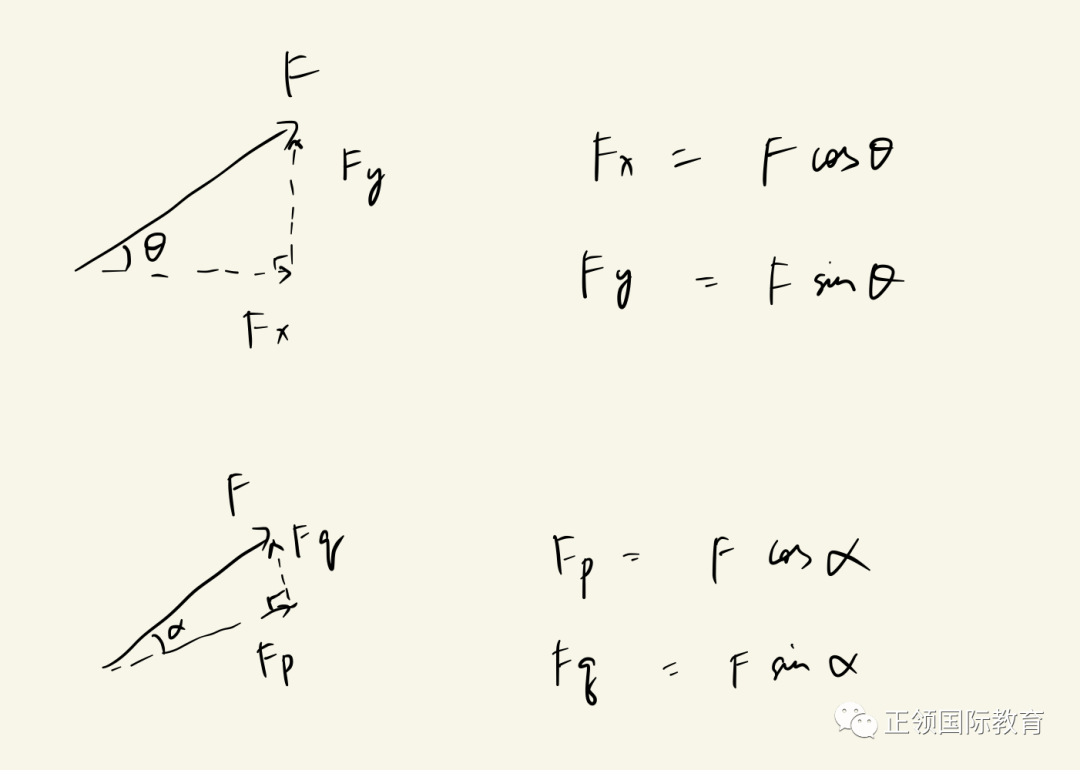
我们可以将力分解成水平方向和竖直方向的两个分力,也可以分解成任意指定方向和垂直于该方向的两个分力(通常用于斜坡问题)。只要F和它的两个分力 构成直角三角形,F为斜边即可。
问题2
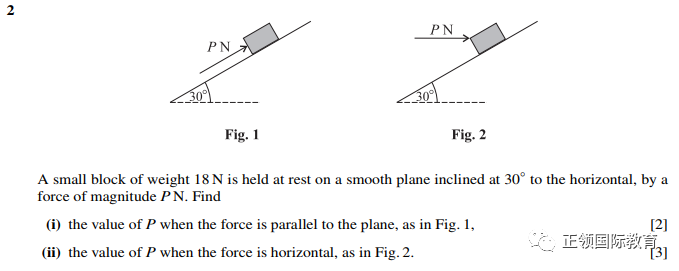
图中物体受到三个力:重力(竖直向下),支持力(垂直于斜坡向上),及P N的推力。我们将力进行分解(平行于斜坡和垂直于斜坡),因为物体处于平衡状态,所以两个方向上的合力均为0,可以列出两个式子。题目中没有要求算R,但是为了方便大家理解,我把R也算出来。

题型三:力的合成
介绍以下两个方法:
方法一(仅适用于求二力合力):画图,平移,用cosine rule求合力大小。
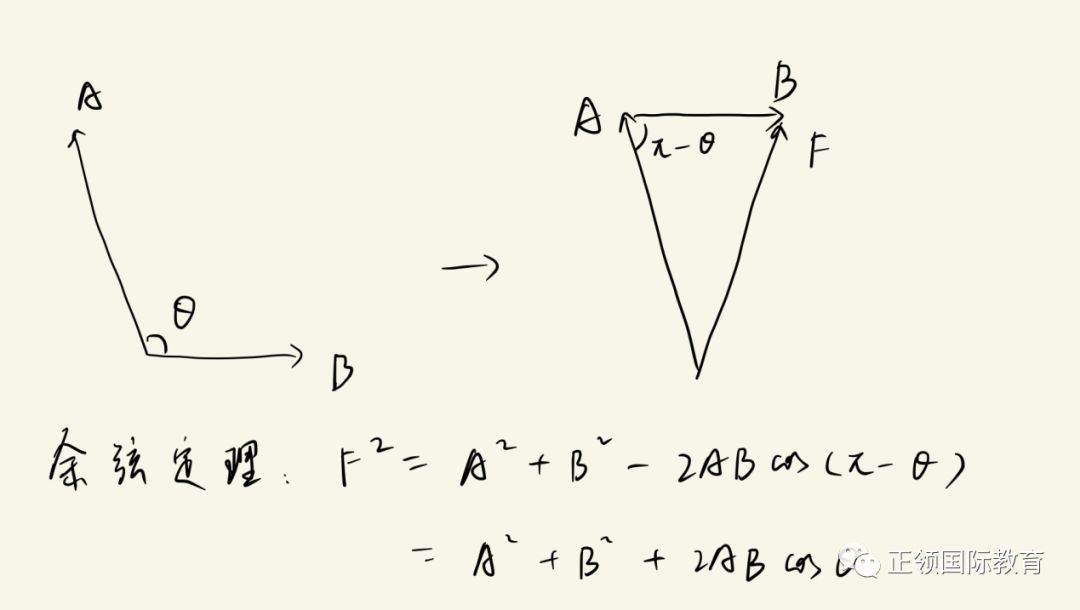
当有三个或三个以上的力合成,我们同样可以通过平移画出合力,却没有办法算出合力的大小,
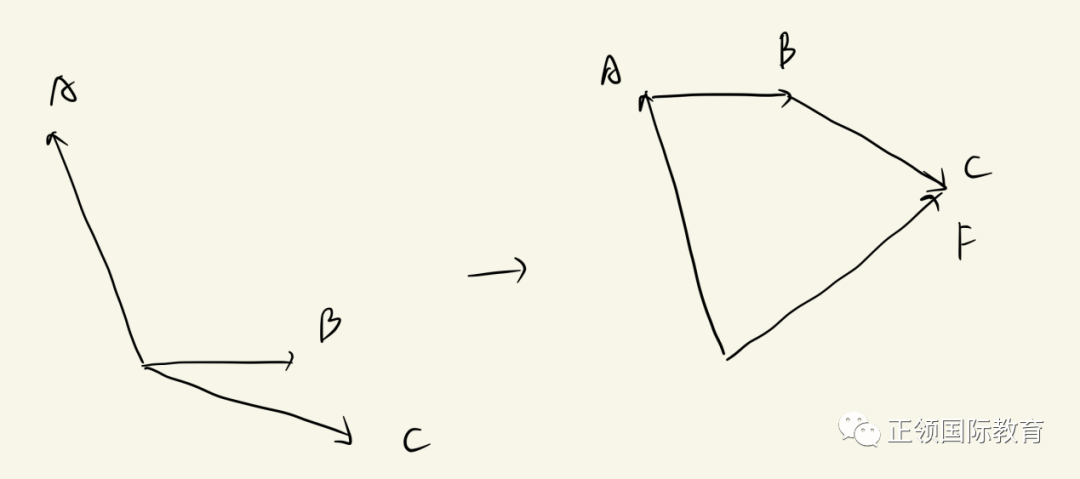
这时候我们要用到方法二(适用于求任意数量的力的合力):将每个力F1, F2, F3, …分别沿x方向和y方向进行分解,再把x方向上的分力相加得到Fx,y方向上的分力相加Fy,最后利用勾股定理和三角函数算出合力F的大小和方向。
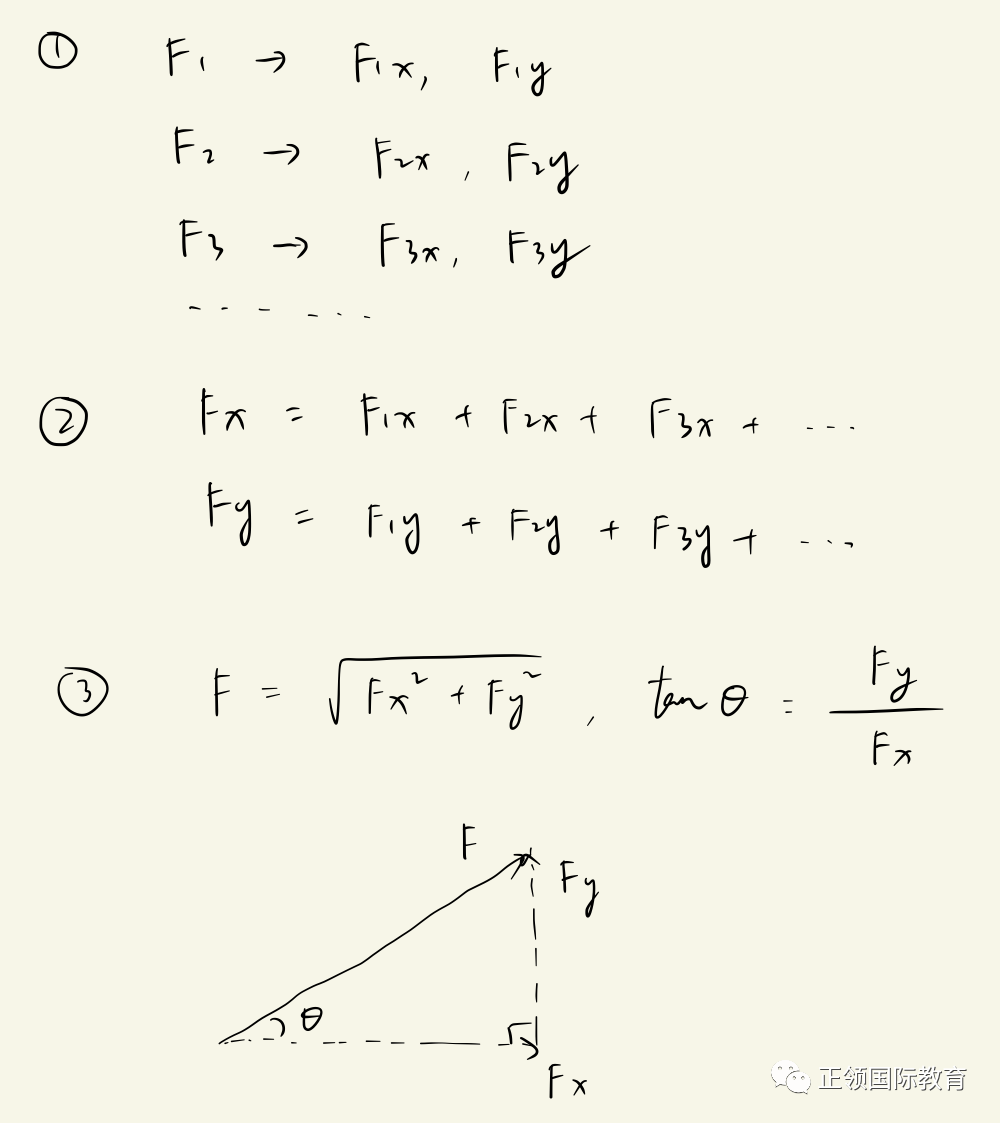
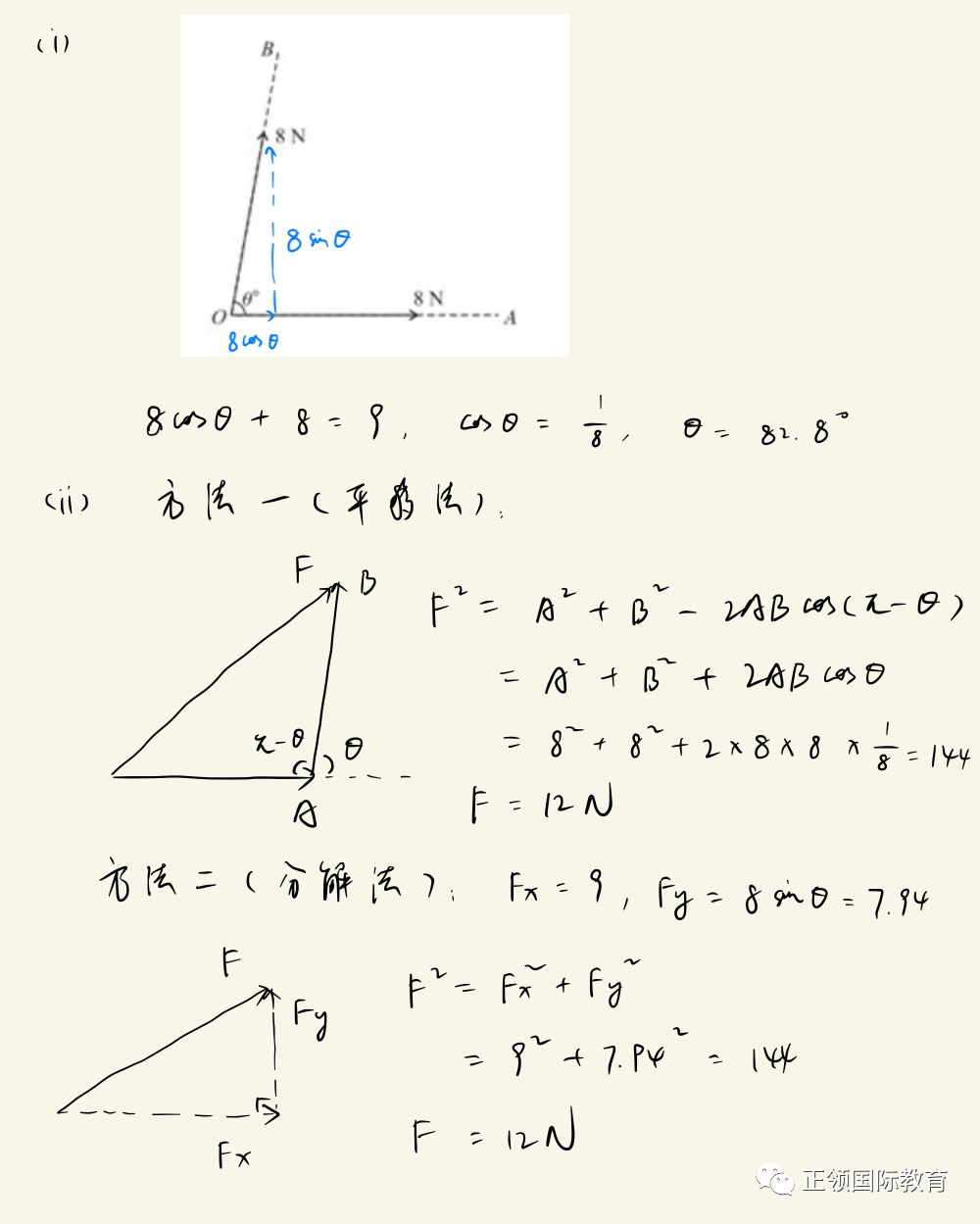
问题3

用上面介绍的两种方法为大家解题:
题型四:三力平衡
这类问题除了运用分解法以外,还可以使用Lami’s theorem,它的好处是不需要分解,直接套公式计算,请注意每个力对应的都是它对面夹角的正弦值。
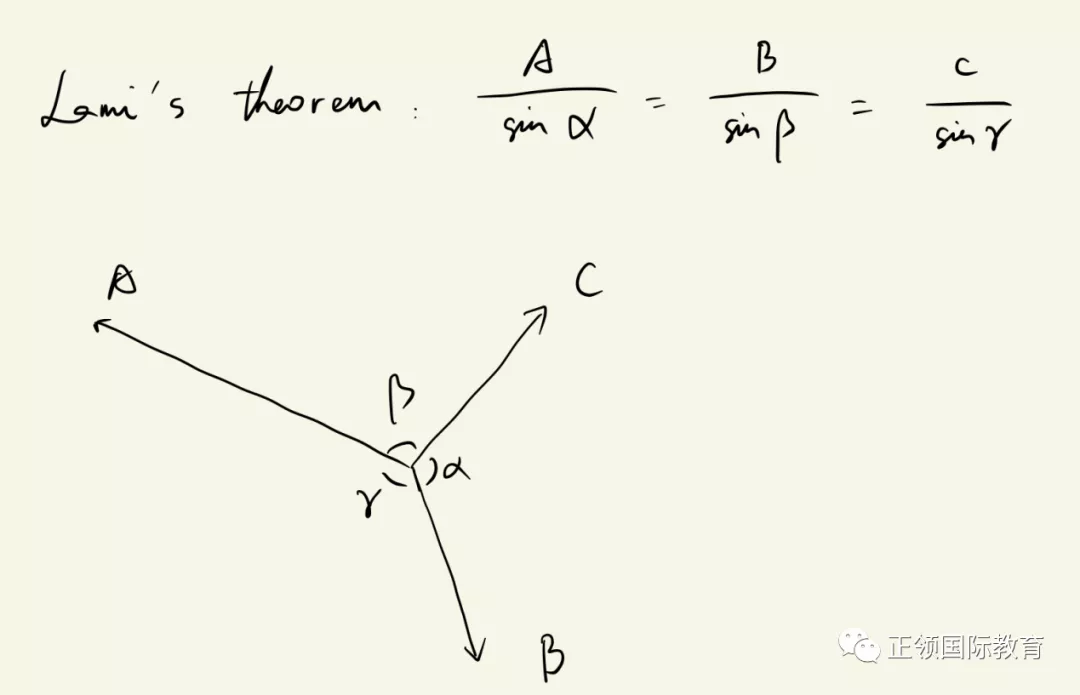
问题4

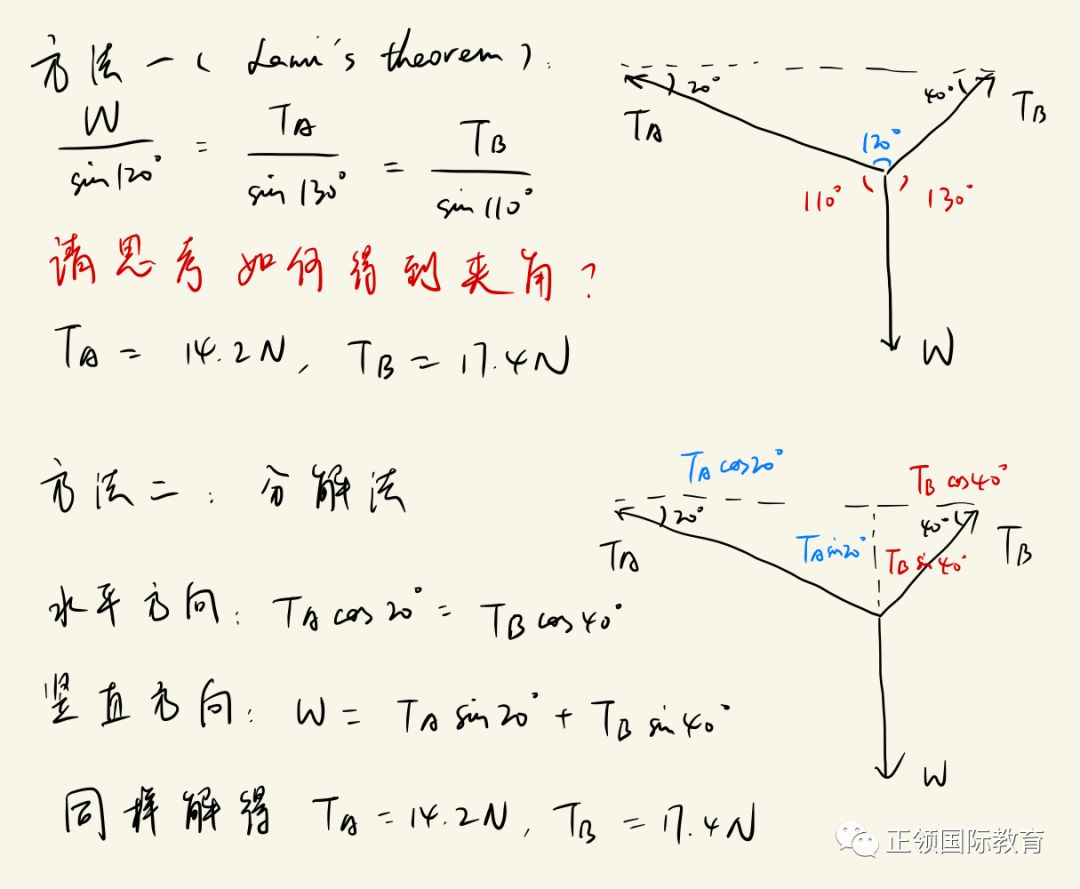
比较两种方法可以发现Lami’s theorem计算更方便。
题型五:非平衡状态
问题5

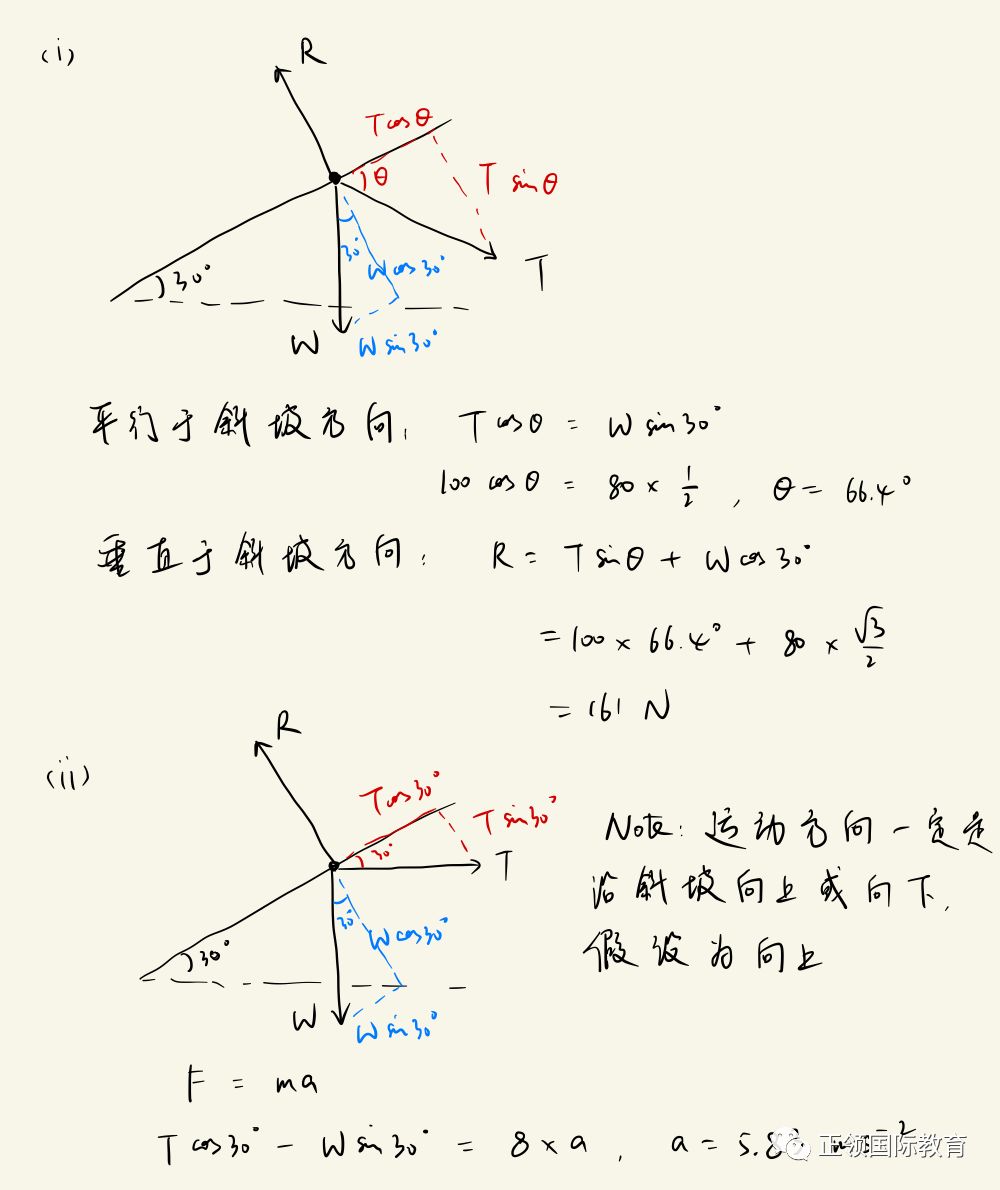
问题6
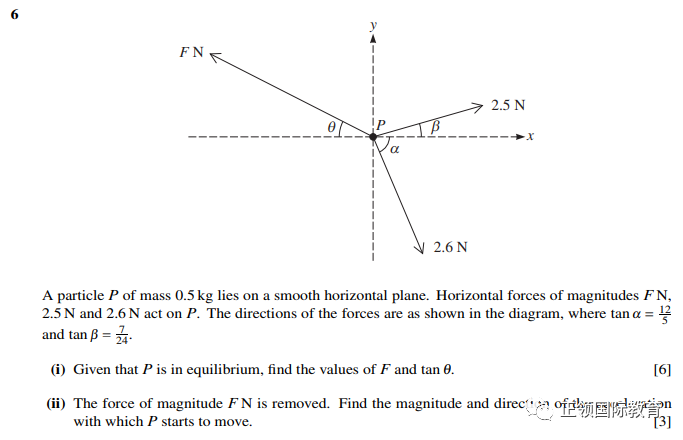


小伙伴看到第一小题的时候也许会有疑问,知道tan的值,是怎么直接得到sin和cos的值?
我们当然可以用计算器按出,以及sin和cos,但请注意这样得到的是近似值,再经过加减乘除也许误差会比较大。以下教小伙伴一个简单的技巧来计算sin和cos的准确值。

今天的题型就讲到这里了,老规矩,练习题如下:





