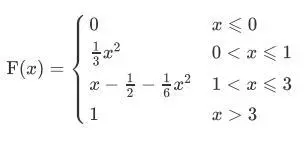2. CDF及其应用

2.1 CDF介绍 

      cumulative distribution function

是个函数

针对连续变量

意义：代表了某个取值x之前所有概率密度的累加

写作：

求法：

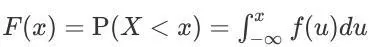
注意该处用大写F的表达与PDF做了区分。

它与pdf的关系即小于x取值的所有概率密度的累加，即变量X最小取值范围到取值x的积分，该积分在书写时注意，定积分范围中包含x, 在这里它代表一个取值的数值，所以在对PDF做积分时，我们要用虚变量(dummy variable) u来替代x，即f(u)而不是f(x)来避免书写错误。

CDF是PDF关于x的积分则一样，将CDF关于x求导即得到PDF的函数解析式。

图像：

CDF的图像叫作肩形线(ogive), 其重要特性是一条单调递增的曲线。Cumulative代表积累，概率密度的累加是一个约来越多的过程，作为PDF的积分，其代表了PDF曲线下的面积。

用一组图来较好的说明：

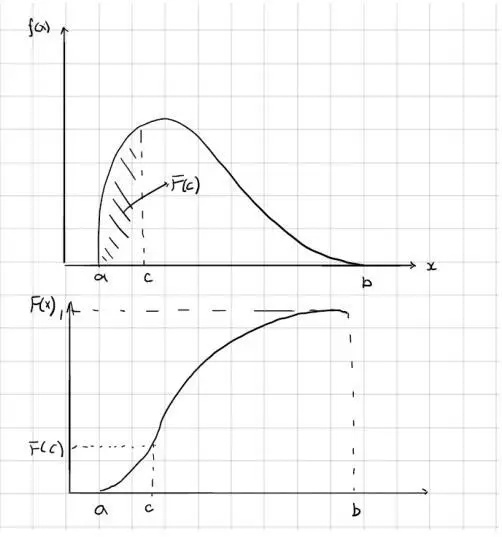
其中第一个图为某连续变量PDF的图像，第二个为其CDF图像。其中图1中的阴影面积代表图2中的c点对应的F(c)。肩形线始终单调递增，其斜率（抖缓程度）和PDF的增长和减少有关，图像中c值前后的变化可以比较明显的对比出来。该变量取值范围ɑ ≤ x ≤ b，最大取值为b，则根据概率基本定义，b处为全段取值的概率积累，即为1。ɑ处概率没有任何累加，即为0。

可总结成，若有PDF:

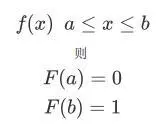
以下用几个例子来阐述CDF在考试中的几种考法和其作用：

2.2 作用1：求区间概率

区间概率：

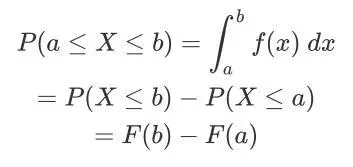
结合图像可以清楚的佐证，a,b区间概率，蓝色部分面积，由橙色斜阴影部分面积 P(X<b) 减红色部分面积 P(X<a) , 结合CDF的定义，可以比较好的理解。

Eg7.

某连续变量X有PDF：

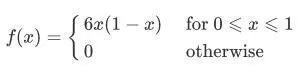
求其CDF: F(x)，由此证，

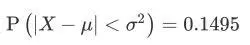
若变量X为正态分布，求：

解

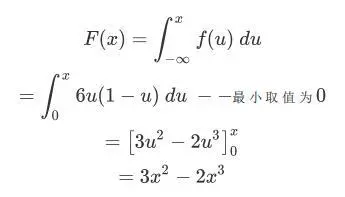
最后CDF写成分段形式,标注取值范围：

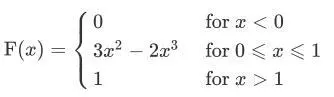
第二部分，求证

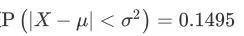
这一部分我们拆绝对值，得到一个关于X的区间概率表达：

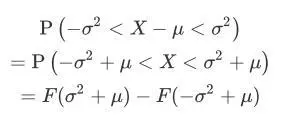
接下来工作就是求：

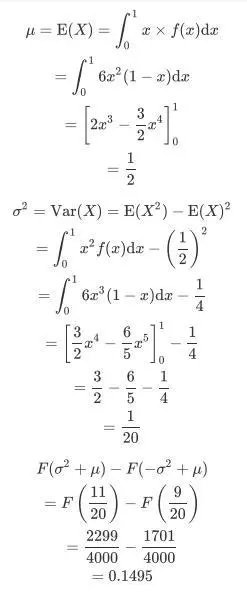
第三部分，对于X为正态分布，区间概率需要先标准化：

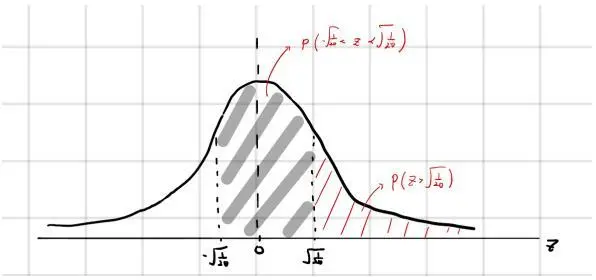
作用2：精准计算百分位数 percentiles

大家应该对频数积累曲线图不陌生(cumulative frequency graph), 其可帮助我们估算(estimate)百分位数(percentiles)

比如下面的这个频数积累曲线图：

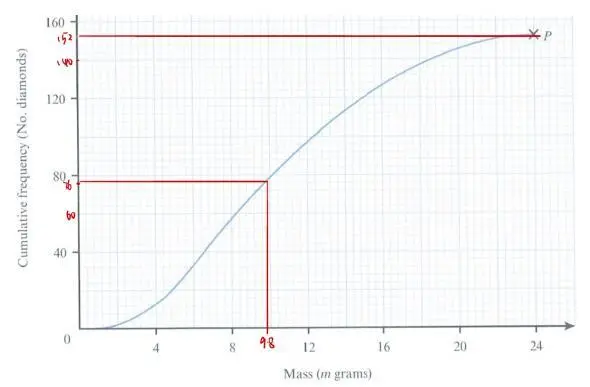
图片来源：Cambridge international AS&A Level mathematics: probability & statistics 1. Dean Chalmers

总积累频数为152，若要求其中位数，或者说是50%百分位数，我们找到其一半的积累频数76，再用尺子水平方向对至频数积累曲线，在其横轴上找到9.8。

注意：频数积累曲线图只能估算百分位数，因为我们需要靠尺子去量取，估算度数等，中间误差不小。

而CDF，可以帮我们精准计算百分位数，两者有精确值上的差别。

例如，中位数，可以理解为50%的分位数(50% quartile/percentile), 根据百分位数的定义：某变量的取值小到大排序所累计概率，某个数据取值点上的概率积累即为这一概率百分比的百分位数。

所以某中位数x在CDF中，可体现为，满足

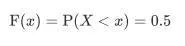
的x值。

Eg8.

有连续变量X, 其PDF为：

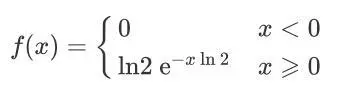
求其四分卫距（interquartile range,IQR）

解：

IQR四分位距的定义为：

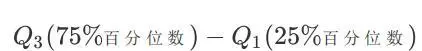
相减的数值。所以本题的关键是求Q₃和Q₁

而求百分位数需要用到CDF。

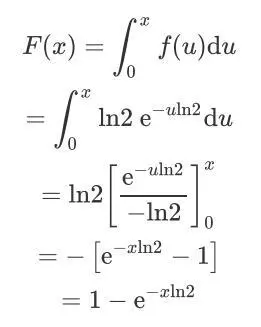
用CDF求得75%百分位数和25%百分位数分别为Q₃和Q₁

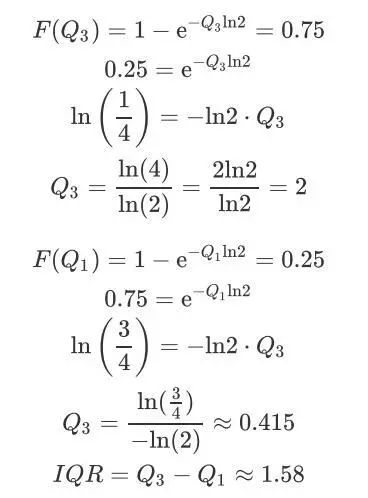
作用3：变量替换

若变量Y是关于变量X的函数，

即 Y = h(X)

已知X的PDF: f(x), 可求得CDF F(x)

求关于Y的CDF(避免重复用其他字母表示):G(y), 

替换的逻辑根据CDF的定义：

Eg.9

某连续变量X有PDF:

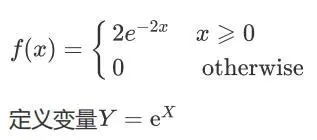
求Y的pdf

解：

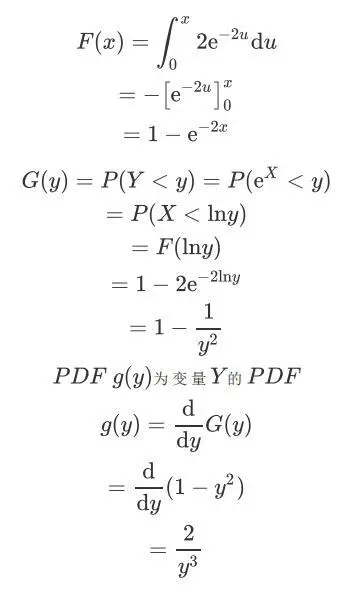
注意变量替换过程中，变量的范围也需要根据替换法发生变换：

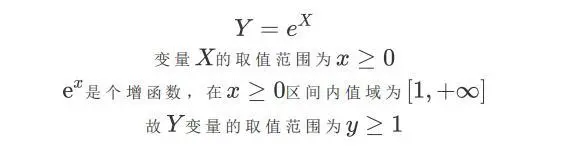
最后y的PDF写成分段形式：

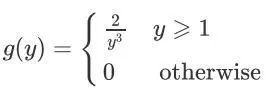
Eg10.

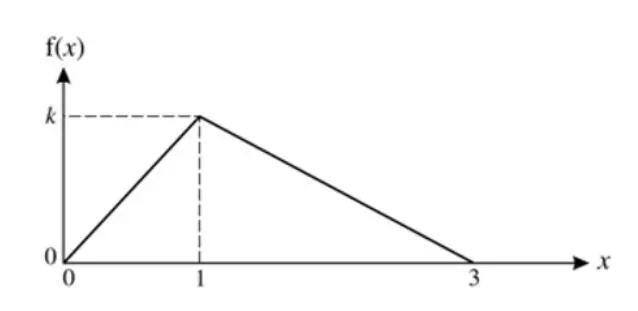
某连续变量X的图像如上，变量X仅在范围0≤x≤3内有取值, 

求证，X的CDF为：

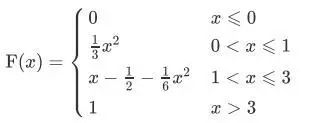
解：

这种分段PDF图像求CDF的题，在教学过程中发现，很多同学都较容易出错。

首先，我们用概率之和为1的概率基本定义求得值，然后在(1≤x≤3段)做积分的时候，CDF为概率积累，而PDF为分段式，读者们不要忘记加上之前部分(0≤x≤1段)的概率积累。

(1) 求k

PDF全段积分之和为1，图中大三角形面积之和为1

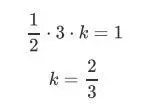
(2) 通过图像表达PDF

(3) 积分求CDF

整合写成分段式，得到结论：