小伙伴们，刚刚结束的A-level数学，大家考得如何呢？

据说今年S1有一个小题是这样的：

Five letters are selected at random from the 9 letters in the word: ACTIVATED.

Find the probability that the selection does not contain more Ts than As.

这道题目是典型用排列组合来求概率的题目。一些同学的答案是这样的：

也就是总数一共66种，符合要求的有41种，所以概率就是41/66。

那么这个答案对不对呢？说实话，如果题目问的是how many possible selections，那么41完全正确。可是这道题目问的是概率，我们就不能直接除了。原因就在于：我们列的这些事件并不是等概率的！

什么是等概率呢？

比如你扔一个均匀骰子，那么扔出1-6的结果都是等概率的，各1/6。但是现实生活中，更多的事件并不是等概率的，但同学往往会忽略。例如，考试只有及格和不及格两个结果，所以及格的概率是1/2吗？更极端的，买彩票只有中500w和不中500w两个结果，难道中500w的概率也是1/2吗？

所以我们S1课本里的这个公式：P=Number of favorable equally likely outcomes/Total number of equally likely outcomes，仅仅是针对等概率事件的，也就是所谓的古典概率。如果用到非等概率事件中去，那一定会出问题的。

图源：网络

再举个简单的例子：如果我们在AAB三个字母里随机挑两个，那么不同的组合有两种，即AA和AB。但要注意这两个组合并不是等概率，我们容易发现，AA的概率是1/3，而AB的概率是2/3。

讲到这里，可能有小伙伴们已经能get到了。那么题目应该怎么去写呢？

记住这点：如果问你组合，两个A是不需要区分的；但如果问你AB的概率，记得要先在两个A里选一个A，然后和B组合。

所以这道考题的正确答案应该是这样的：

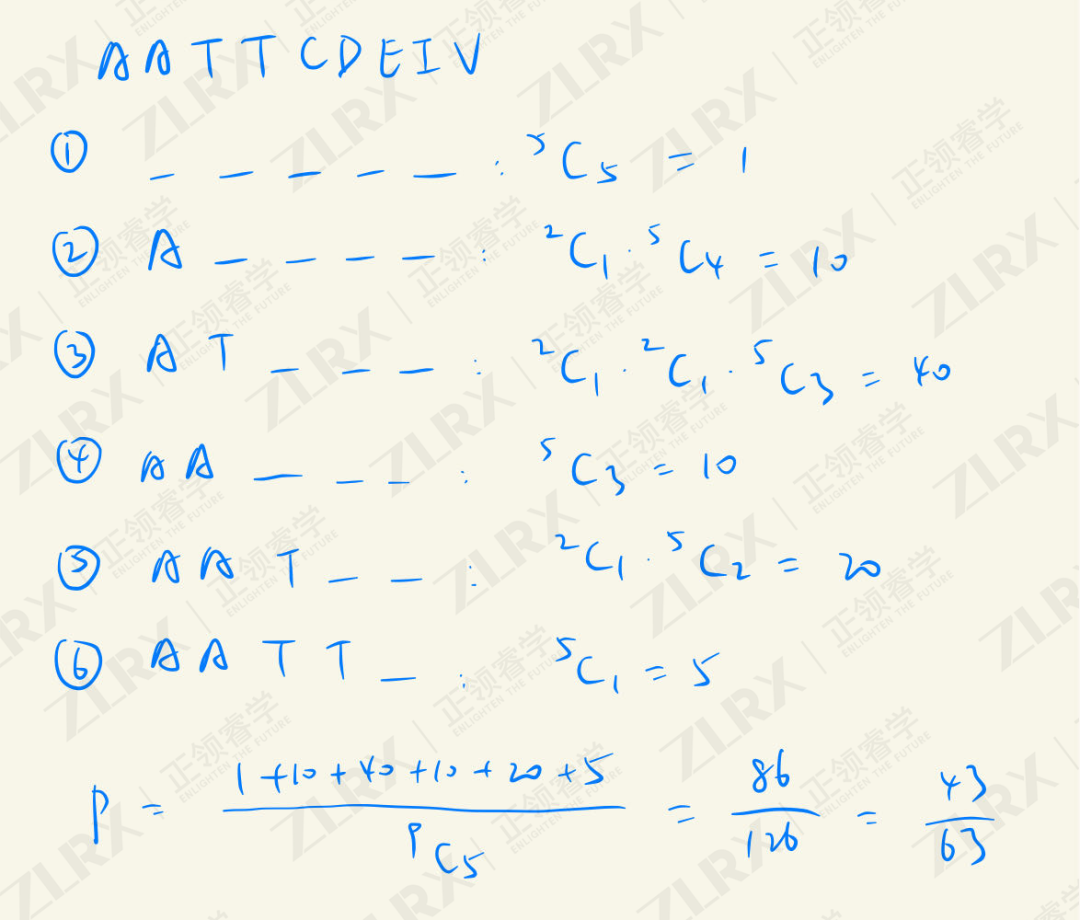
当然，考试已经告一段落，纠结答案也无意义。只是希望小伙伴们在今后的学习中不要仅仅会背公式，而要理解原理，不然很容易用错。

另外，明年的考生们，如果还没有学到S1这部分内容，可以先学起来啦，如果已经学到排列组合，一定要把这个题型吃透哦！