嗨!同学们好,我就是大家的江老师。
下是我为大家准备的试题解析。在这里先提前跟你们“约法三章”——同学们先自己思考题目,试着做一做,然后再对答案哈。
小编偷偷告诉你们:其实江老师很年轻的!
以下试题排版都是:
先试题题目和答案截图
然后是老师要点分析
1

分析:
本题考查基础的二项展开公式,x项前系数为负,注意计算问题
第二小问:

第二问为二项展开常见题型,在原展开式之前乘以一个关于x的多项式,注意事项请看上面解题步骤。
2

分析:
本题第一问考查链式法则,注意题目中的表达准确找出对应数学关系,比如the rate change of x, the rate change of y, increasing at a constant rate等。
3

分析:
第三题考查用积分求原函数,注意在p1中分母为关于x的多项高次式时,不要将其展开,作为一个整体进行计算,具体步骤如上,注意题目要求什么,将答案写完整。
4
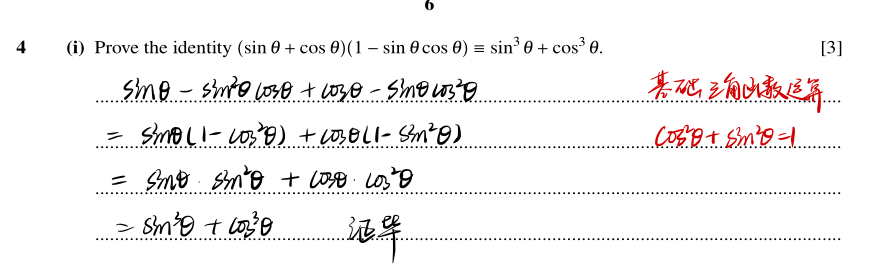
分析:
本题为三角函数基础,把握住sin,cos之间的关系即可。
第二小问:
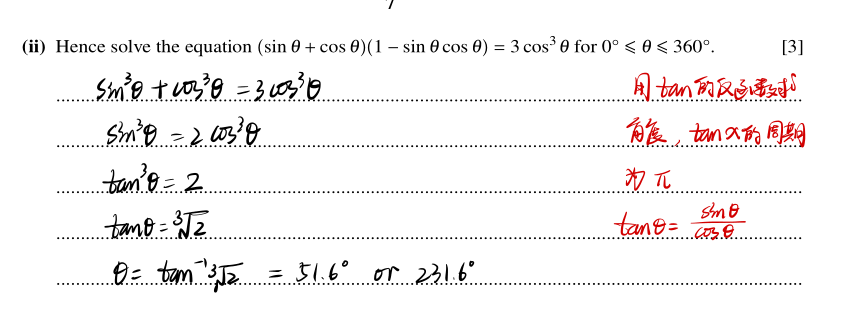
第二问运用sin,cos,tan的关系即可解出,还有使用三角函数反函数求角度的应用,注意角的domain,0到360度则要考虑三角函数的周期性,tan以π为周期。
5
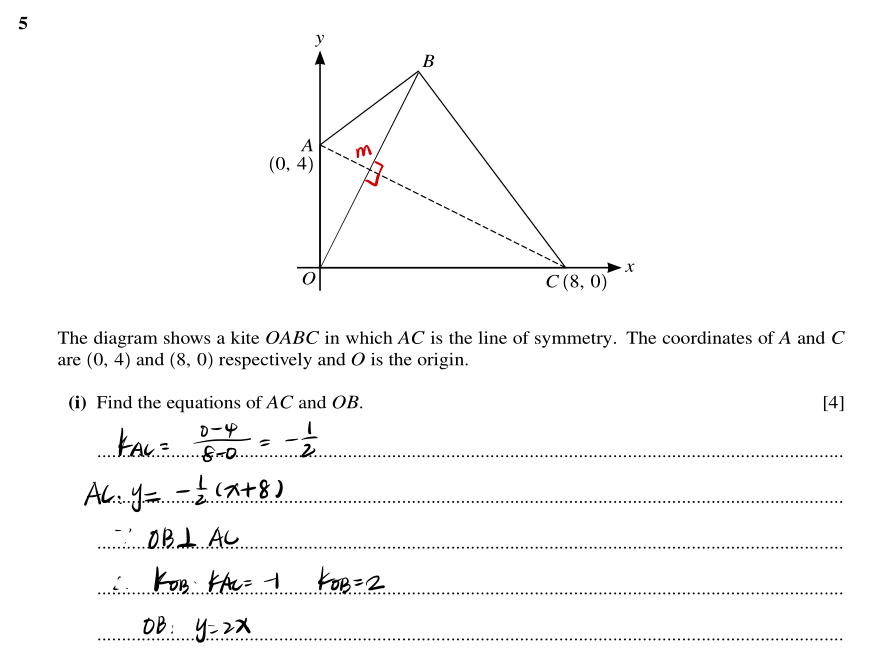
分析:
坐标系,点,线的基础题型,牢记出现垂直相交的两条直线时运用斜率乘积为-1的特性,两点求直线方程,点斜式求直线方程都要牢牢掌握。
第二小问:

第二问先用两直线方程联立求出交点坐标,再用中点坐标公式求出中点坐标,千万不要用距离公式去求点的坐标。
6

分析:
考查弧度的应用,扇形面积的求法,理解弧度制和圆的关系即可,灵活运用三角函数。
第二小问:

第二问主要难点在求弧长,斜边长仍然用三角函数求出。
7

分析:
向量基础运算,没有难度
第二问:

第二问考查三个知识点,向量的数乘,向量的加法以及单位向量的求法。
第三问:

第三问考查向量点乘的两种计算方式,一种坐标相乘,一种几何算法,向量的模乘积乘以其夹角的cos值。
8

分析:
等比数列,当|q|< 1时,无穷等比数列的求和公式
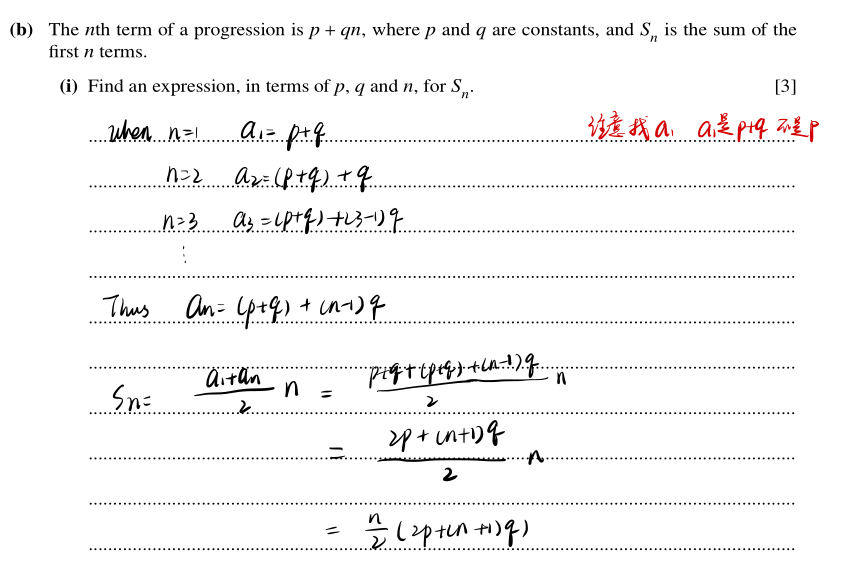
第二小题注意找a1,Sn使用求和公式即可。

第三问,简单将数据代入求和公式,联合建立方程即可。
9

分析:
联立方程,用因式分解解出答案。
第二小问:

第二问考查inequality,记住口诀,大于取两边,小于取中间。
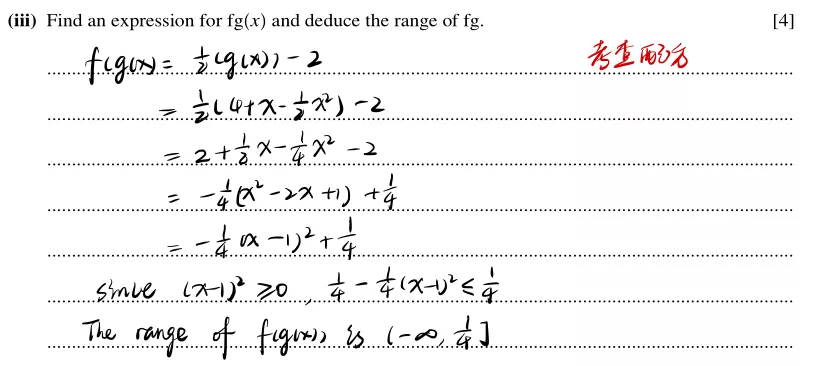
第三问考查配方法,即可直观的求出该函数的range
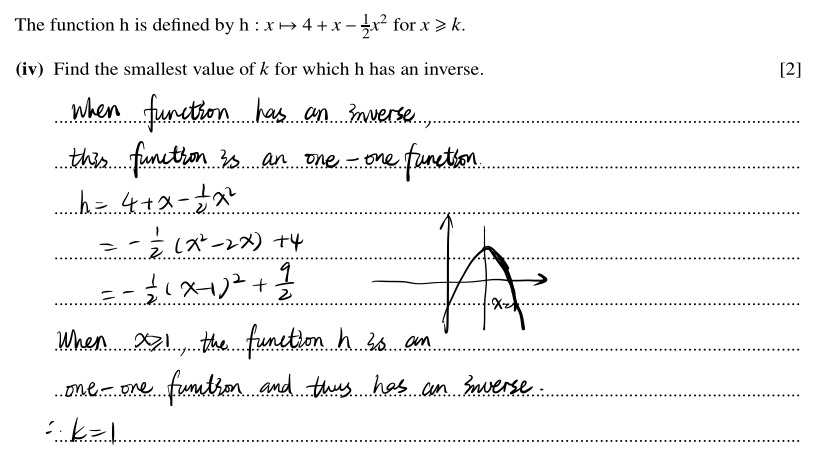
第四问考查反函数的定义,必须是one-one function才有反函数
10

分析:
该题考查微分,明白微分的几个性质,1. 微分=0,即函数在该点切线的斜率;2. 微分> 0,即函数在该点为increasing function;3. 微分< 0, 即函数在该点为decreasing function。
第二小问:

第二问结合二次微分考查微分的性质,一阶微分为0时,二阶微分>0,该点为最小值点,二阶微分<0时,该点为最大值点。
第三小问:

第三问考查使用定积分求旋转体体积。
好了以上就是江老师为大家整理的试题了。




