在A-level数学课程中，Quadratic function二次函数一直都扮演着很重要的角色，涉及到的题型也非常的多样化，不同版本的教科书都在一开始或者前几章就会学习Quadratic function的知识点, 每年真题中也会有对二次函数的考察。

首先，让我们来看看Quadratic function二次函数的形式：

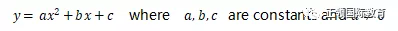
(同学们肯定对二次函数很熟悉，这里就不多做介绍)

我们经常会看到 solve the equation 或者 find the solutions. 当x=0 时，我们很容易能找到y=c,  但是当y=0是，我们需要会解= 0时x的值。 

今天这篇文章就来罗列一下二次函数的三种解法，并且讲解一下不同的解法是如何以不同的形式出现在真题中的, 主要是希望能帮助同学巩固一下二次函数知识点。

1. Factorization 因式分解法

 Factorial form    y=(x-r)(x-s)

把一个多项式化为几个最简整式的乘积的形式，二项式通常放在等式左边，每个因式（x-r）和（x-s）中x的次数一定要低于原来的二项式，分解到不能再分解为止。

真题中的出题类型：解不等式的时候会用到因式分解的知识。

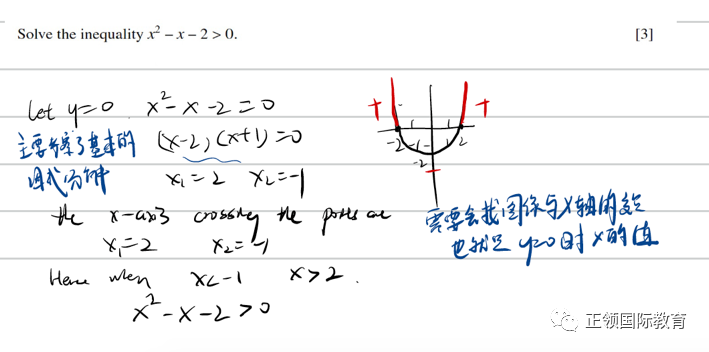
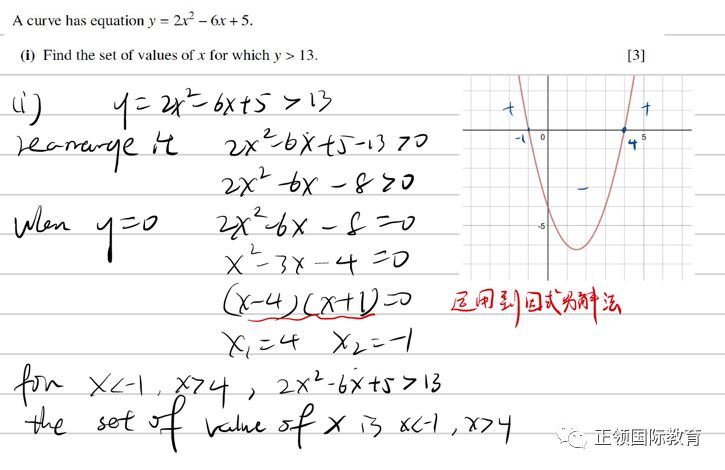
Tips：

遇到二次函数先把所有项放到左边并尝试能否拆成2个数的乘积。因式分解法能将函数快速拆分开找到x的值，但是很多时候函数比较复杂并不能拆成很明显的乘积，遇到这种情况我们可以直接用公式法求解。

2. Completing the square  完全平方法

Completed square form（我们也可以叫做vertex form）

 真题中的出题类型：画图要求vertex时，也就是求minimum／maximum point时。题目直接写明y=a(x-h)2+k形式时。

Tips：

completing the square 多数运用在找最大或者最小值时，有时候我们会在题目中看到直接写明 in the form  y=a(x-h)2+k或者写成completing form。其他情况能用因式分解的就用因式分解。

3. The quadratic formula 二次公式法

真题中的出题类型：判断或者题目中出现找roots时。找line和curve的交点时。

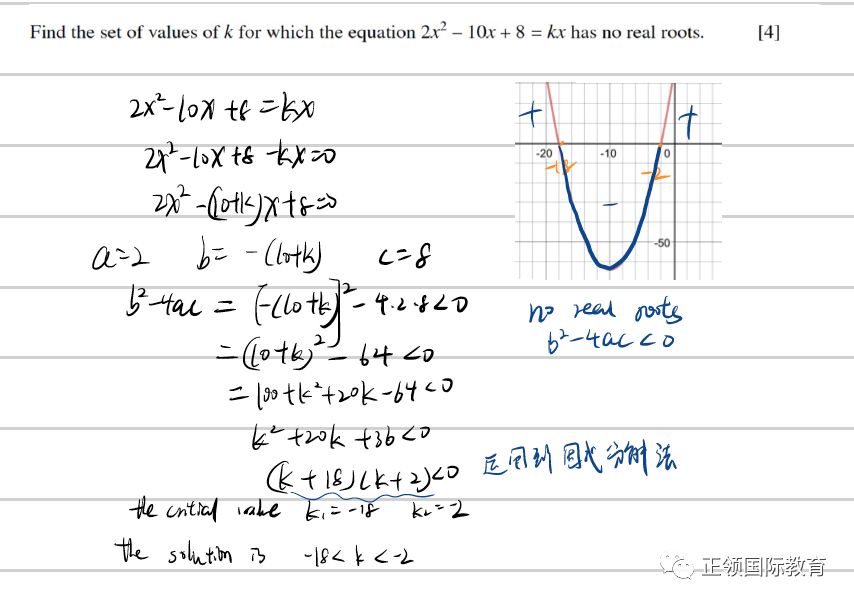
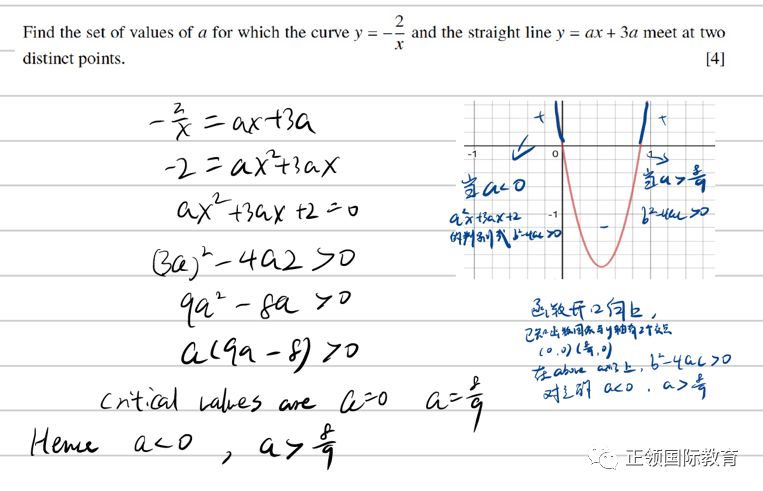
Tips：

公式法能解所有的二次方程，但是如果能直接用因式分解法时最好直接用因式分解法。题目中看到求curve和line的交点时需要用到来判断根(关键词：tangent，no common roots, not meet, distinct roots. etc）题型都很类似，需要同学们多多练习。

教材很多其他章节都会交叉涉及到二次函数的运用，真题同一道大题里的每一道小题也会交叉涉及到二次函数不同的解法，在这边只能作简单的概括。同学们只要多刷题巩固好二次函数知识点，融会贯通，碰到新题型时就能快速准确地解出。