上一篇文章最后提到了有大量函数的不定积分不能用初等函数表示，或者通俗地说，很多函数的积分是“积不出来”的。如果放眼整个函数库，“积不出来” 的情形要比 “积得出来” 的更多。

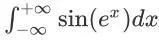
先尝试求不定积分，做一次替换，

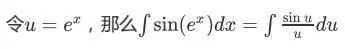
可惜右边的函数依然 “积不出来”

那是不是不定积分求不出来，定积分就一定没法算呢？答案是未必。

再看一下它的定积分，

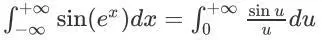
神奇的事情来了，

右边这个定积分竟然是可以算的！

我们目前所学的知识还不到位，必须要借助高深的大学数学的方法。如果你的目标只是应付考试，那么今天的内容你可以忽略。但如果你想走进大学数学的大门，了解数学分析究竟是怎样的，进而领略数学的美，我相信，读完今天的文章对你一定是有帮助的

狄利克雷积分

Dirichlet Integral

这是一个很有名的广义积分：

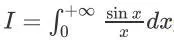
在很多领域有着重要应用

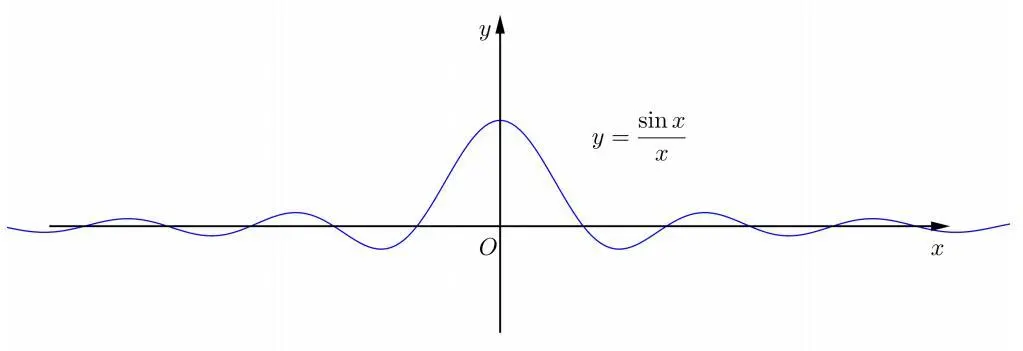
广义积分是对普通定积分的推广，就像这种含有无穷上限或者下限的积分，我们称为无穷限广义积分， 它的收敛性是需要证明的。

狄利克雷判别法

1、多重积分方法

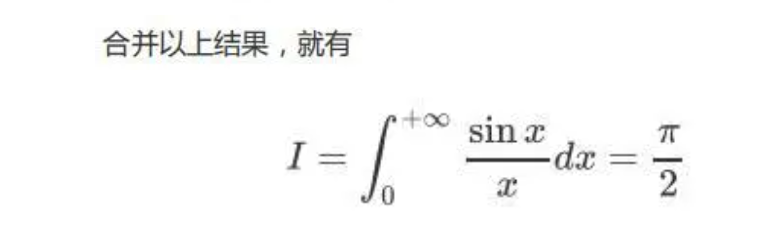
2、复变函数方法

相比第一种方法，第二种方法可能更深奥一点，其实它的思路就和高数中complex summations类似，即我们在求实函数的定积分时，可以转化成求复函数的曲线积分，最后取实部或虚部。

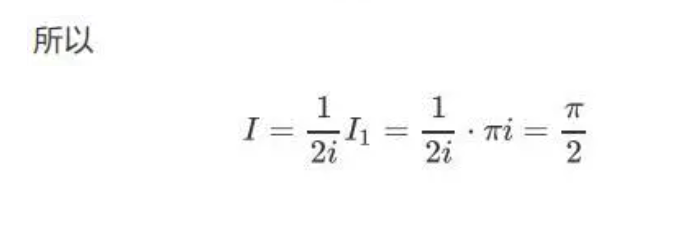
今天介绍的两种方法，大家都看懂了吗？

看懂的话那恭喜你

你已经具备进入数学系的潜质啦！

看不懂也没关系

最起码你把结论记住

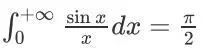
平时和小伙伴们吹吹牛装装b还是可以的。当然除了上述两种之外，还有更多的方法，如Fourier变换、Laplace变换等，感兴趣的小伙伴可自行查阅文献。

高中数学和大学数学最大的区别在于，高中数学着重于计算，只要会做题目就万事大吉，而大学数学放眼于分析和证明，即便掌握了一个命题的证明思路，那也是最基本的要求，还要尽最大努力去揣摩这些命题的证明思路是怎么想到的。