现在离s1的考试只有三天的时间，同学们想必已经胸有成竹了吧。在考试的前夕，江老师就带大家一起来梳理s1的知识点让大家做到查漏补缺，冲击满分。

S1

10月份s1考试可以分为5个部分：

1. Representation of Data. 

2. Permutation and Combination. 

3. Probability. 

4. Binominal Distribution. 

5. Normal Distribution. 

通过今天的梳理，希望大家能够对这五个知识点做到了如指掌。

Representation of  Data

该章主要讲了，数据类型（types of data）,茎叶图（steam-and-leaf diagram）,直方图（histogram）,箱线图（box plot），累计频率分布图（cumulative frequency graph）和主要的统计指标，中位数（median），众数（mode），平均值（mean），方差（variance）以及分位数（quartile）。

这个章节应该掌握的是上述四种图的画法，注意茎叶图需要写key，back-to-back steam-and-leaf diagram的key的写法，关于直方图的题看清题目给的是frequency table还是frequency density，箱线图的画法，两组数据的箱线图记得画数轴，不要只摆着两个箱线图在那里。茎叶图，直方图，箱线图的优缺点也需要回顾并记住。

关于统计指标的计算没有难点，但注意不要带入错误数据，inter-quartile range的求法（Q3-Q1），这个指标通常用来measure spread，Q2就是median。还有outlier的范围：

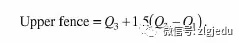
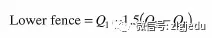
这两个指标不常考，但别忘了怎么计算。

最后则是mean和variance的计算，不熟练的趁这几天多做做题巩固一下。

Permutation and Combination

这个章节考的比较活，主要注意的是读懂题目，注意C和P的关系，需要顺序的，比如说坐座位，排几位数，或者看到arrangement，arranged，seated，with order之类的词汇，就要反应过来是排列，排列涉及的方法有：

1、整体法

比如两个或多个物体需要紧挨着放置，就可以将这两个或多个物体视作一个整体再和其他元素去排列，需要注意的是，整体内部的物体也需要排序，还要注意整体内部和其他元素是否有重复的，注意计算。

2、插空法

这种方法适用于元素和元素不能紧挨着放置，可以将其他没有限制的元素先排列，再在元素之间插入不能放置在一起的元素，变种考法会限制首位元素，或者末位元素，这会使可插入的空挡变少，注意计算。

3、分类讨论法

对于不同类别分类讨论，最后将每一类的排列数加和为最后结果，这种题型会有点绕，但是同学们细心的分类就没有什么问题，题目会分的类别也不会太多，一般在3-6类左右。

含重复元素的排列，需要除以重复元素个数的阶乘（factorial）。

以上所提及到的方法会组合出题，灵活运用所学知识。

组合则是不看重排序，只看重元素，相同元素不论怎么排序，都是同一种组合。比如，选committees成员，从一类东西中选择几个出来组成另一种组合，这些都是组合类型的题。

Probability

概率的难点仍然在于读题，理解清楚题目的意思最为重要，需要掌握的知识点有：

1、概率的范围（值域[0,1]）   

2、当A，B互为对立事件时P(A)+P(B)=1, P(A)=1-P(B),这个关系在很多题中（包括概率，二项分布，正态分布，排列组合等）都有用，比如求P(X>3), 就可以用1-P(X≤3)来计算。

3 、当A，B互为独立（independent）事件时,P(AB)=P(A)*P(B),这个公式也可以用来检验事件A，B是否independent。

4、会考察probability distribution table，在这个表中，所有probability加起来等于1，这是一种检查手段。

5、会算expectation（期望）和variance（方差），s1中只会考离散变量：

6、会算exapectation（期望）和variance（方差），s1中只会考离散变量：

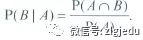
Binominal Distribution

记住使用二项分布的4个条件，有一年的真题考察了这个知识点：

1.There are N repeated independent trials.

2.N is finite.

3.There are just two possible outcomes for each trial.

4.The probability of success in each trial, p is constant.

对于二项分布而言，最重要就是两个参数，n和p，只要找到这两个参数，二项分布的题将迎刃而解。必须记得二项分布的期望/均值（mean）（np）和方差（np(1-p)）。

二项分布会结合概率进行考察，比如二项分布中的p会通过条件概率去求，或者p需要通过另外的二项分布求出等等。还会结合正态分布一起考，正态分布可以作为二项分布的approximate distribution。

Normal Distribution

最后的最后，便是正态分布，在s1中正态分布需要掌握的便是读表和标准化，找出相应的概率，完成题目。

若标准化后的z值或者求出的概率（反推z值）不在表中（表只能查到小数点后三位），则可以找与它临近的两个值，使用linear exploration，去找这个z值的正态分布概率，比如对于z值0.9034，不能在表上查到，我们需要通过表上的两个点（0.90,0.8159）和（0.91，0.8186）去找0.9034所对应的的概率，通过这个式子（相当于求直线上的点）便可以算出我们需要的概率值。

需注意的是，正态分布表中的概率为

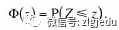
若想要求P(Z>z),则需要通过去求，还有一个重要等式：

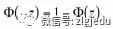
去年S1的难度有所提升，反应在题目的灵活性方面，但是解题方法永远不会超纲，只要认真审题，仔细做好每一步，相信同学们拿到高分是轻松加愉快。

还有三天就要进行战斗，希望同学们都能打一个漂亮的胜仗！！