同学们明年开始就要开始用新考纲了，尤其是向量部分的考点也会变很多。

这一次的P3考试将会是老考纲的绝唱，为了防止它离开之前给我们沉重的打击，我们要对考纲烂熟于心，现在就让我们一起看一看吧。

01 Algebra

1.绝对值函数

绝对值函数有三种常见的解法：

(i) 分类讨论法，较多用于解不等式。根据不同的区间，来消除绝对值，并加上正负号。

(ii)平方法，左右两边同时取平方，将绝对值消除，然后解方程得到答案。

这二种方法适合较简单的题型,例如真题9709/31/M/J/17的第一题：

(iii)图形法，将函数图像画出，然后根据特殊点坐标来解题。

适合用于解较为复杂的题目，例如将积分与绝对值方程结合的题目，例如真题9709/31/M/J/19的第一题：

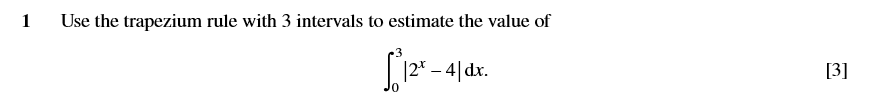
(iii)图形法，将函数图像画出，然后根据特殊点坐标来解题。

适合用于解较为复杂的题目，例如将积分与绝对值方程结合的题目，例如真题9709/31/M/J/19的第一题：

2.多项式

求多项式的系数有三种方法：

(i)长除法：和除法一样，较为简单。

(ii)配平系数法：当已知多项式的一个因式的时候，可以设另一个因式的系数为a,b，然后展开，根据多项式的系数来求a和b的值。

(iii)试验法：如果题目信息量不足以做题，可以尝试这个方法，任意取一个数，多为得到多项式的一个根之后，再进一步的化简。

考试中要根据题目信息的不同，来选择一个最简单的解题方式！

3.部分分式

分式分解的题目比较简单，记住书上的公式，用配平系数法即可。

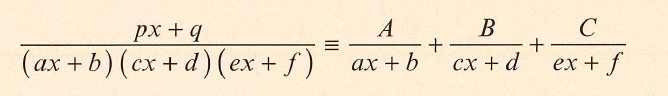
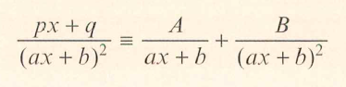
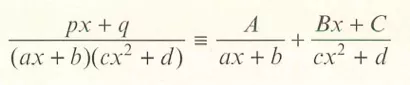
例题可见9709/31/M/J/2019的第八题第一小问：

4.二项式展开

二项式展开要应用公式表上的公式，题目中出现的时候不一定是这种形式，但一定要提出一个常数k，使得括号内变成的形式，且常数k提到括号外之后变成k^n。

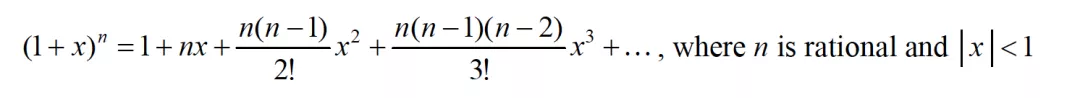
9709/31/M/J/2019的第八题第二小问就是一个很好的例子：

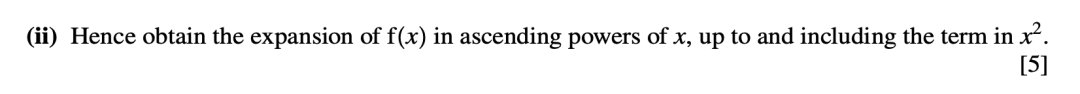
在这道题目中，第一小问的分式分解有三个项，需要分别代入二项式展开公式，计算量极其大，所以常常会出现计算错误，考试中一定要小心！！！

02 Logarithmic and exponential functions

对数和指数函数常见的题型有：

1、指数函数等式/不等式求解

(i)替换法，例如设，先解出u的值，再算x的值，例题可见9709/32/M/J/10第一题：

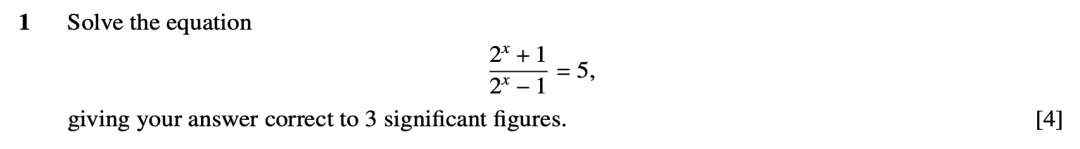
(ii)用对数函数来将指数函数化简，得到一个关于x的等式，然后求解，例如9709/31/O/N/14的第一题：

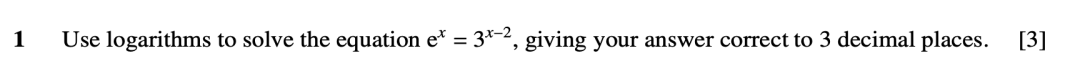
2、对数函数等式求解

先运用对数函数的运算法则，将等式同侧的项合并或者分解，然后等式两边同取指数形式，将对数消除，例题可见9709/31/M/J/19的第二题：

3、指数函数化简成直线

这种题型是指数函数等式求解的特殊题型，考试出现的并不是很多，但也要掌握技巧，做法与之前的做法类似，将方程化简成直线形式，再利用与y轴交距来解常数的值，真题例如9709/33/M/J/10的第二题：

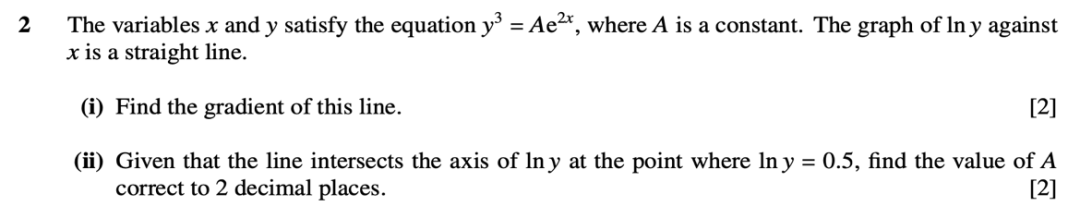
03 Trigonometry

三角等式的化简

这种题型难度不是很大，合理的运用加角和二倍角公式，将等式化简成为一元二次方程的形式或者直接可以解出未知数的值。

对应的真题如9709/03/O/N/04:

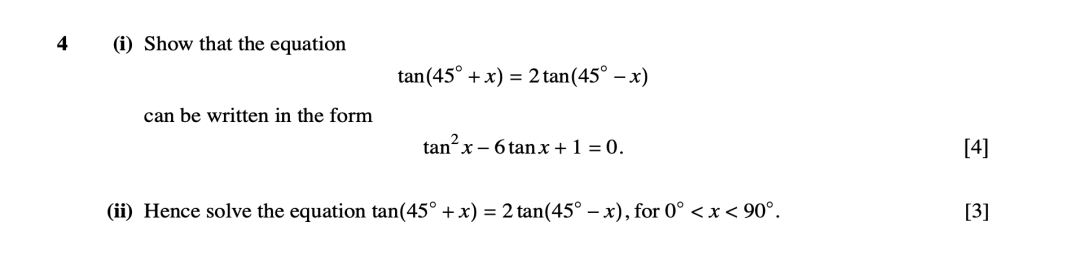
三角恒等式的化简以及证明

三角恒等式的化简例如asin⁡θ±b cos⁡θ=c可以化简成R sin⁡(θ± α)的形式，公式如下：

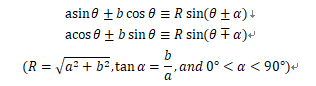
例题可见9709/33/M/J/13的第四题：

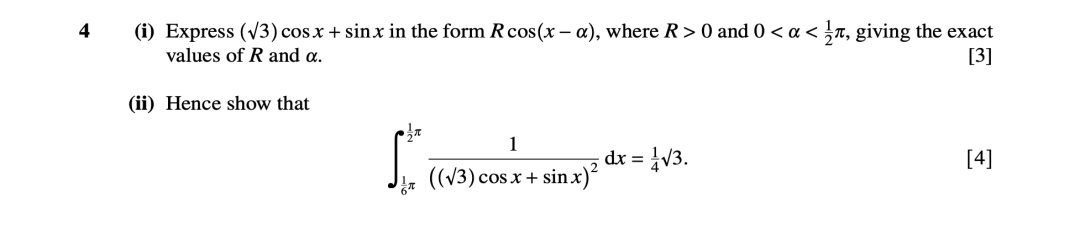
此外，还有一种题目是要求证明一个三角恒等式，需要注意的是此类题目的第二小问往往会伴随着对该恒等式的应用。

例如用这个恒等式去算积分，与积分结合的题目难度可以变得很高，所以此类题目需要多加练习，典型的例题有9709/31/O/N/12的第五题：

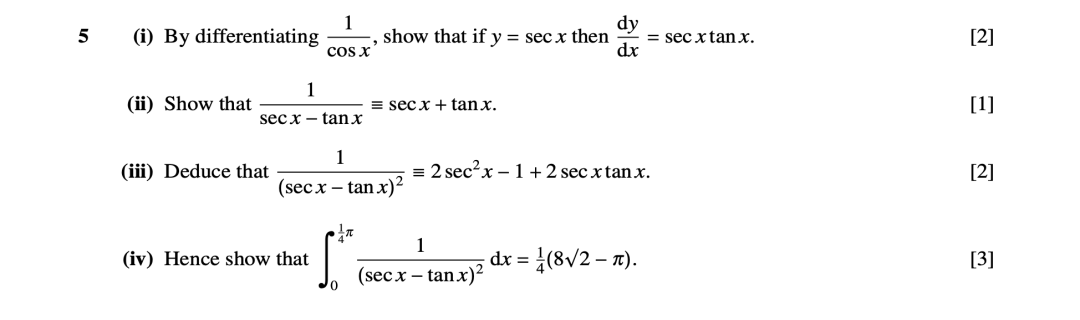
04 Differentiation & Differential equation

对于微积分，我们一定需要记住的三个Rule:

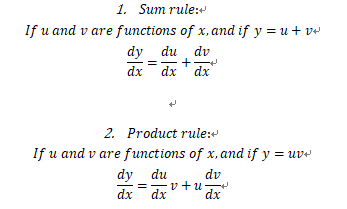
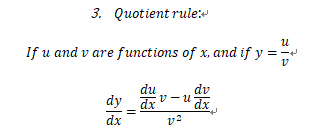
与此同时，我们也需要知道对于参数方程与隐函数如何求导：

1、参数方程求导

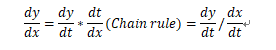
例题可见9709/22/O/N/16的第七题：

2、隐函数求导

隐函数求导需要结合Chain rule与Product rule,将每一个关于x的项求导，再用Chain rule对f(y)求导得到f^' (y)  dy/dx的形式。

隐函数求导有两种方法：

(1)隐函数对数求导法则：

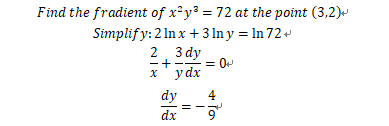
(2)对每一项对x进行求导：

真题可见9709/31/O/N/12的第七题：

3、微分方程

微分方程常见的考题需要学生能够根据题目中给的信息来列出微分方程，常见解题步骤：

(1).分离变量：

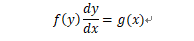
(2).两边同时积分：

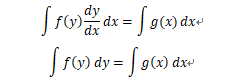
(3).解出通解

(4).根据给的条件得到具体解，看一道比较典型的例题9709/3/O/N/08的第8题：

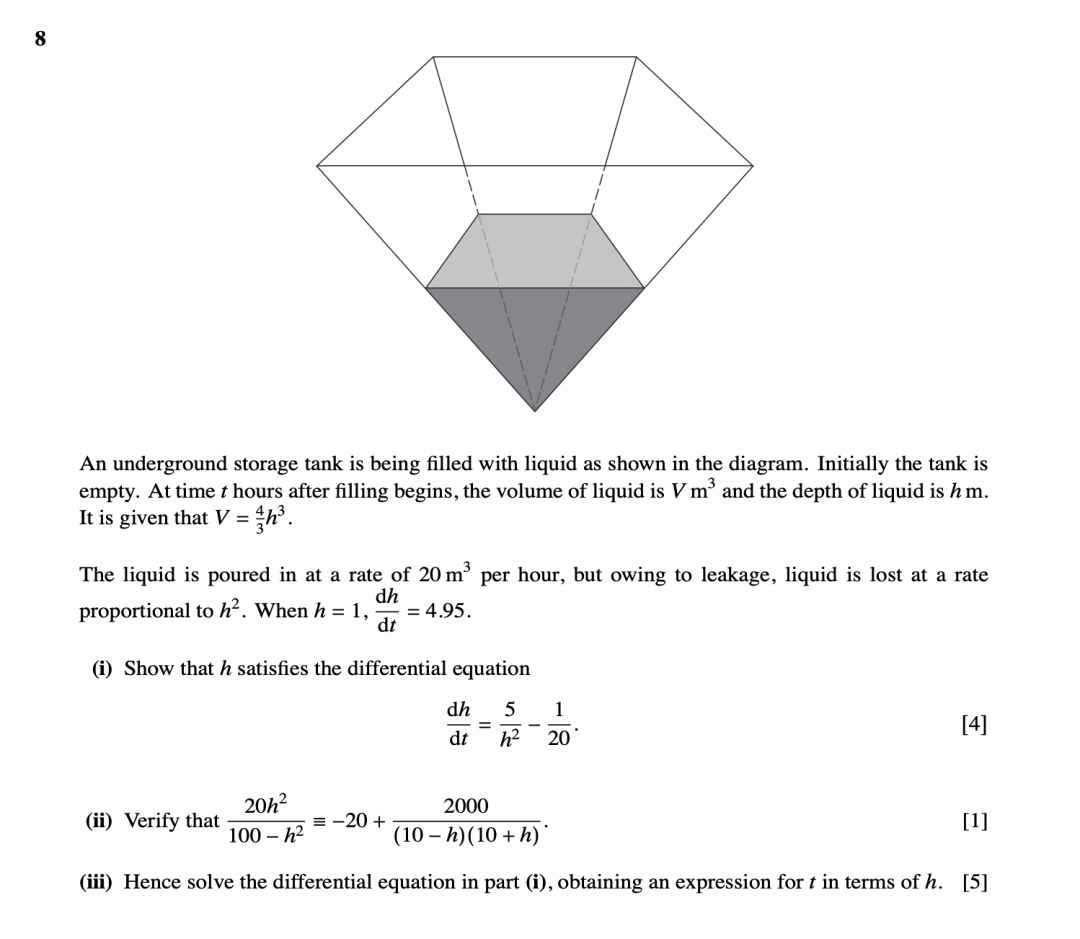
以上就是考纲的前4个部分，还有4个考纲内容后期再跟同学们讲解。