同学们昨天讲了P3考试老考纲的前4个考点部分,没看的同学点击"干货|| A-Level数学P3老考纲最后一次登台(上)”
今天就继续讲剩下的4个考纲部分内容。

A-Level数学老考纲
虽然目录大纲都一样,但是有些考试考点却发生了变化,不知道同学们有注意到没有?(图片可点击放大查看!)
05 Integration
积分这一部分往往在考试中难度较大,我们来归类一下可能出现的题型:
(1) 积分与三角函数的结合:
可以回看第三部分Trigonometry的第二小部分。
(2) 积分与有理函数的结合:
这种题目,我们需要用partial fraction的知识点,将式子化简,然后再积分。
经典题目参考9709/33/O/N/16的第6题:
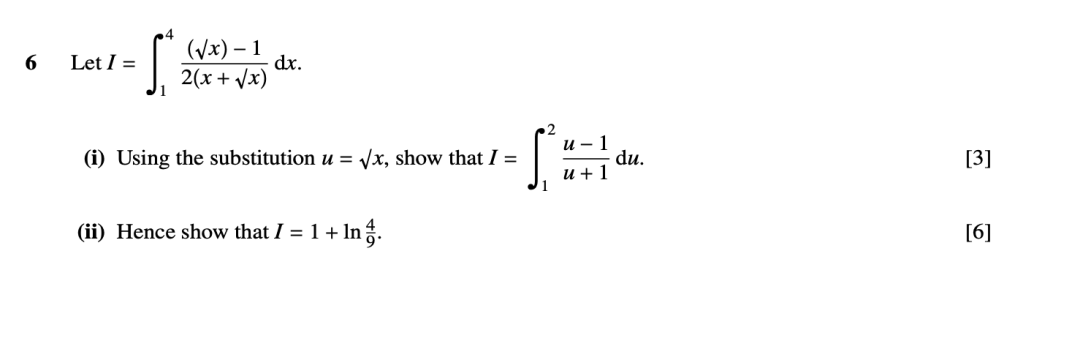
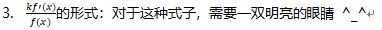
(4) 分部积分:
分部积分难度可能会较高,需要多加练习,例题如9709/32/M/J/11的第十题:
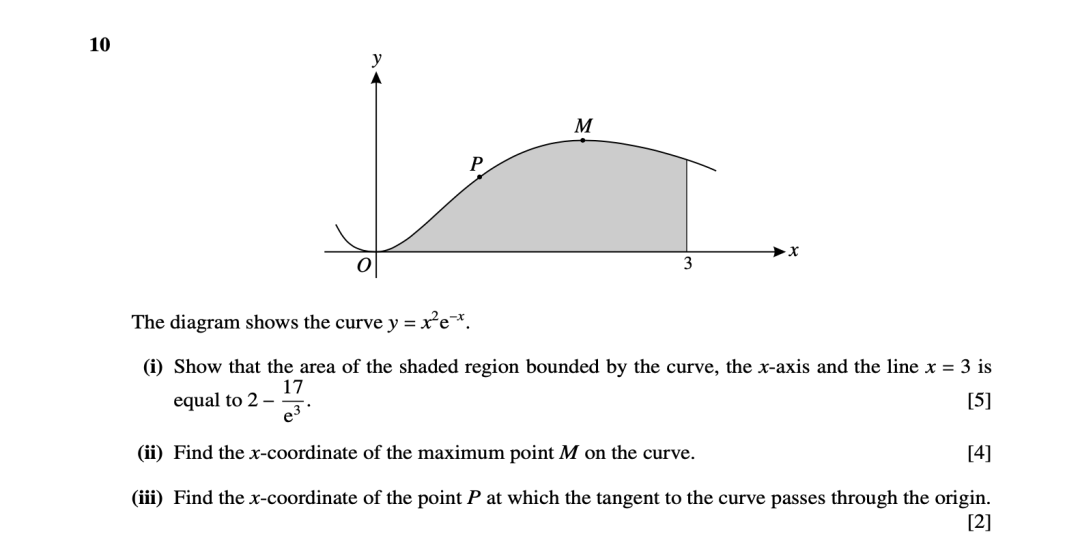
(5) 代入法:
代入法一般情况下题目都会给提示,所以不是很难,按着题目给的提示一步一步做即可,看一道9709/03/O/N/05的第六题:
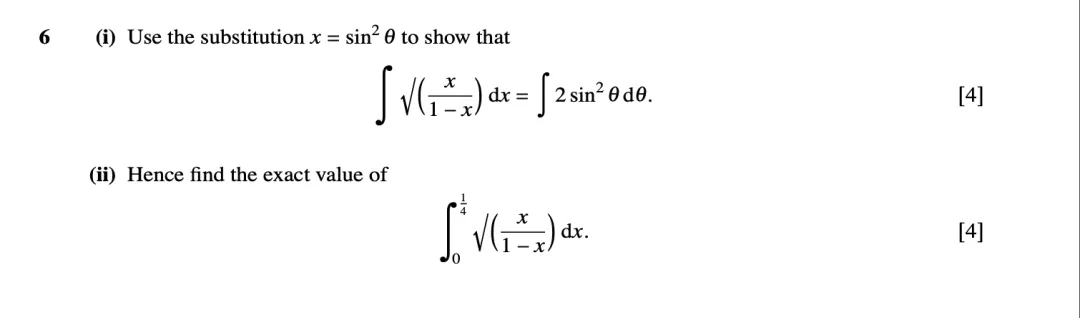
(6) 梯形法则:
梯形法则也较简单,如果有些遗忘可以看之前写的2019年P3-31卷解析里的第一题,有详细的解题思路与答案解析,可以再去翻一翻。
06 Numerical solutions of equation
(1) 利用函数变号来证明区间内存在根:
Sign-change rule:
If the function f(x) is continuous in an interval of its domain, and if f(p) and f(q) have opposite signs, then f(x)=0 has at least one root between p and q.
(2) 用迭代法来解方程:
利用迭代公式:多次迭代,得到方程的解。考试中用计算器的时候可以利用Ans键更快的得到答案。
07 Vectors
向量在真题中经常出现的题型有:
求平面方程
(1) 一点一线求平面:
一点一线求平面,用点与线上任意一点,得到一个向量,再求这个向量与线的方向向量的向量积,化简后带一个点进去,得到平面方程,可以参考9709/3/M/J05的第十题第三小问:

(2) 两线求平面:
两条线求一个平面,只需要求两条线的向量积,选取一个特定点即可得到平面方程。
例题如9709/31/M/J/10的第十题第三小问:

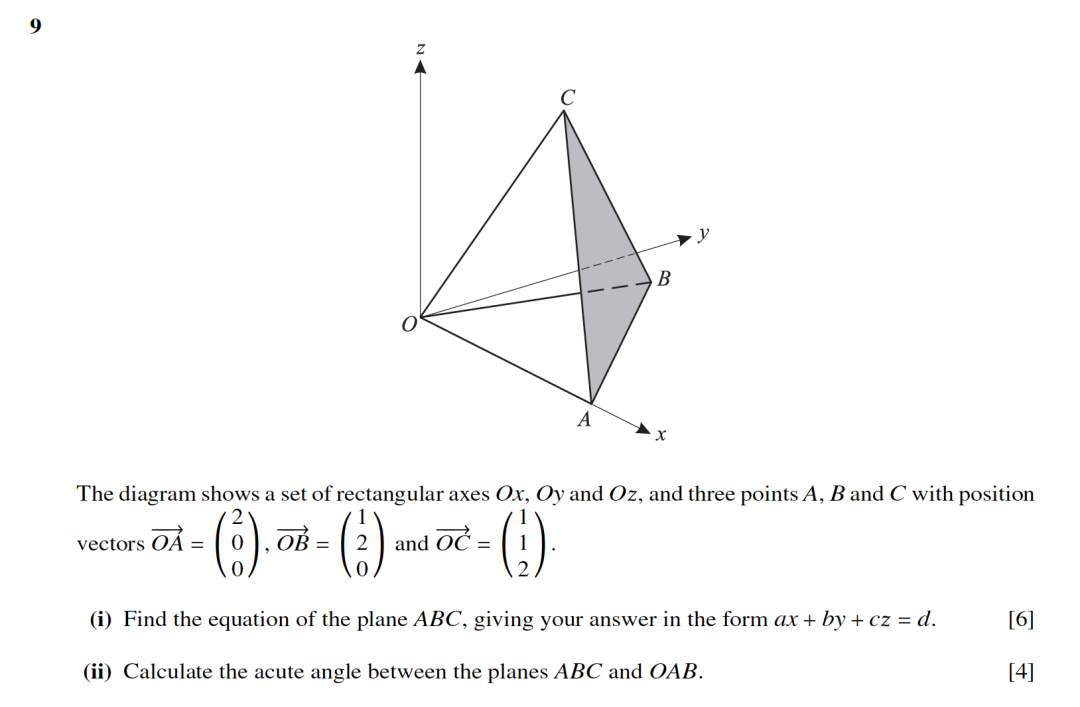
(3) 三点求平面:
三点求平面与两线求平面类似,由三点找出两条线,再用两线求平面的方法,就可以解题。
可以看例题9709/03/M/J/06的第十题的第三小问:

求距离
(1) 两点求距离:
两点间距离可以找出两点的坐标,然后求两点向量的模。例题有9709/32/M/J/10的第九题第二小问:
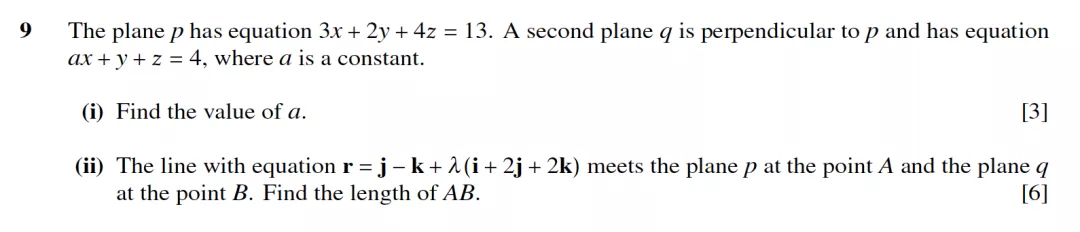 (2) 点到线的距离:
(2) 点到线的距离:
点到线的距离要首先找出点到该线的垂足(用数量积即点乘公式),然后求向量的模。参考9709/3/O/N/02第十题第三小问:

(3) 线到面的距离/面到面的距离:
这种情况较为复杂,不同的题目要根据给的条件来决定解题思路,可以参考一下例题9709/33/O/N/11的第9题(线到面的距离):

以及9709/31/M/J/2017(面到面距离):

求夹角
求夹角的题目都用点乘来做,选取两条合适的线,求出夹角,再根据情况来算题目中所要求的角度。
(1) 一线一面求夹角:
9709/33/O/N/10的第6题:

(2) 两面求夹角:
9709/03/M/J/07的第9题:
08 Complex numbers
(1) 复数的运算法则:
单纯的运算较为简单,这里就不赘述了。
(2) 复数的模以及辐角:
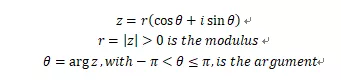
另外需要注意的就是模-辐角形式下的乘除法:
To multiply two complex numbers we multiply the moduli and add the arguments.
To divide two complex numbers we divide the moduli and subtract the arguments.
(3) 多项式的共轭根:
使方程 p(z) = 0的非实数根总是以共轭根的形式出现。当你算出一个非实数根的时候不要遗漏的它的共轭根,例题如9709/31/M/J/2019的第十题中的第二小问:

(4) 复数的极坐标形式以及运算:
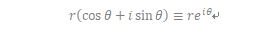
与第二部分类似,但考试常考,以上文同一道题目的第一小问为例:
 (5) Argand diagram:
(5) Argand diagram:
画图可能以方程或者不等式的形式出现,找出对应的部分之后不要忘了标注,以上文同一道题目的第三小问为例:

A-Level数学P3的考试所有大纲考点都在这里了。这些都是我们薛老师为大家整理的考点,记得收藏起来,好好复习和巩固这些知识点。




