在Quadratics这一章我们需要学会的知识点：

解二次方程

解联立方程

找最大最小值

判别式的应用

NO.1

首先我们要知道二次方程就是指含有一个未知数并且未知数项的最高次数是2，经过整理都可化成一般形式ax²+bx+c=0。在这里我们可以用以下三种不同的方法来解二次方程。

方法1: 因式分解 (Factorisation)

Step1: 把方程整理成ax²+bx+c=0

Step2: 将方程左边分解为两个一次式的积。

Step3: 将这两个一次式分别为0，得到两个一元一次方程

Step4: 解一元一次方程，得到的解就是原本二次方程的解。

那我们从具体的题目中来看如何用这些步骤：

方法2: 完全平方法(completing the square)

什么是完全平方？把ax²+bx+c转换为a(x+p)²+q

如何变成完全平方的形式？

我们需要用到以下两个公式：

 x²+2dx=(x+d)²-d²

 x²-2dx=(x-d)²-d²

用这两个公式我们就可以快速有效的把一般二次式转换为完全平方式啦，接下来我们可以通过一个例子更好的学习这个方法。

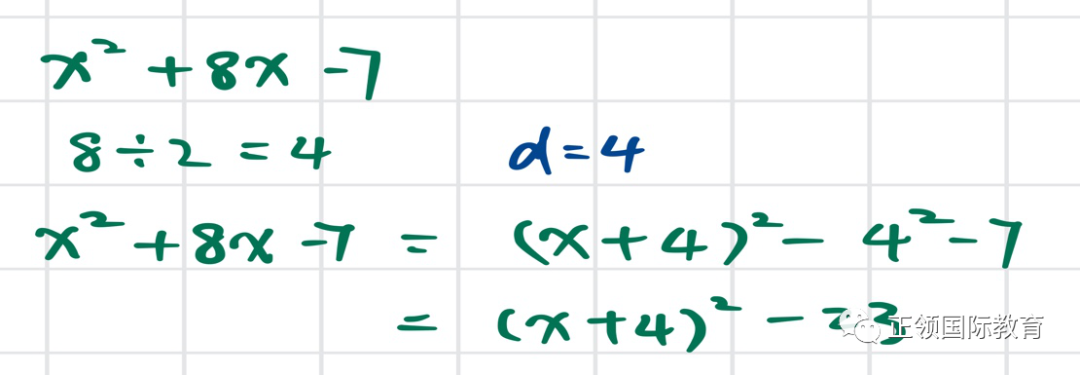
那转换为完全平方有什么好处呢？

1、画图；

2、找最大最小值；3.找二次式的反函数。这些都将在之后的学习中体现出来。

方法3: 公式法（quadratic formula）

这个方法适用于解任何一个二次方程, 所以一定要熟记这个公式。

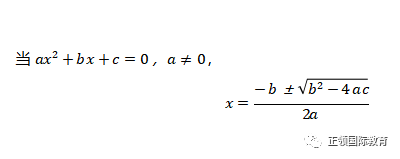
对如何得到这个公式感兴趣对同学可以看一下它的证明：

简单的举个例子，套用公式就可以非常快速的得到两个解啦：

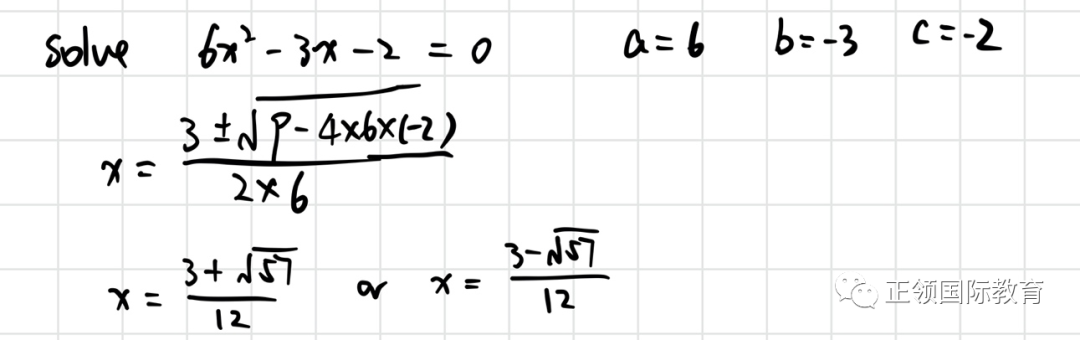
总的来说，只要我们熟练掌握这三种方法，就可以解任意一个二次方程啦～

NO.2

除了学会如何解二次方程之外，我们还需要会解有关二次方程与线性方程的联立方程，也就是找到两个方程的交点。

举个例子，有一个二次方程y=x²-4 和一个线性方程 y=2x-1,我们需要去解这个联立方程，也就是找到他们的交点A,B. 如图所示，我们可以得到A(3,5) B(-1,-3), 所以联立方程的解为x=-1, y=-3 或者x=3,y=5。

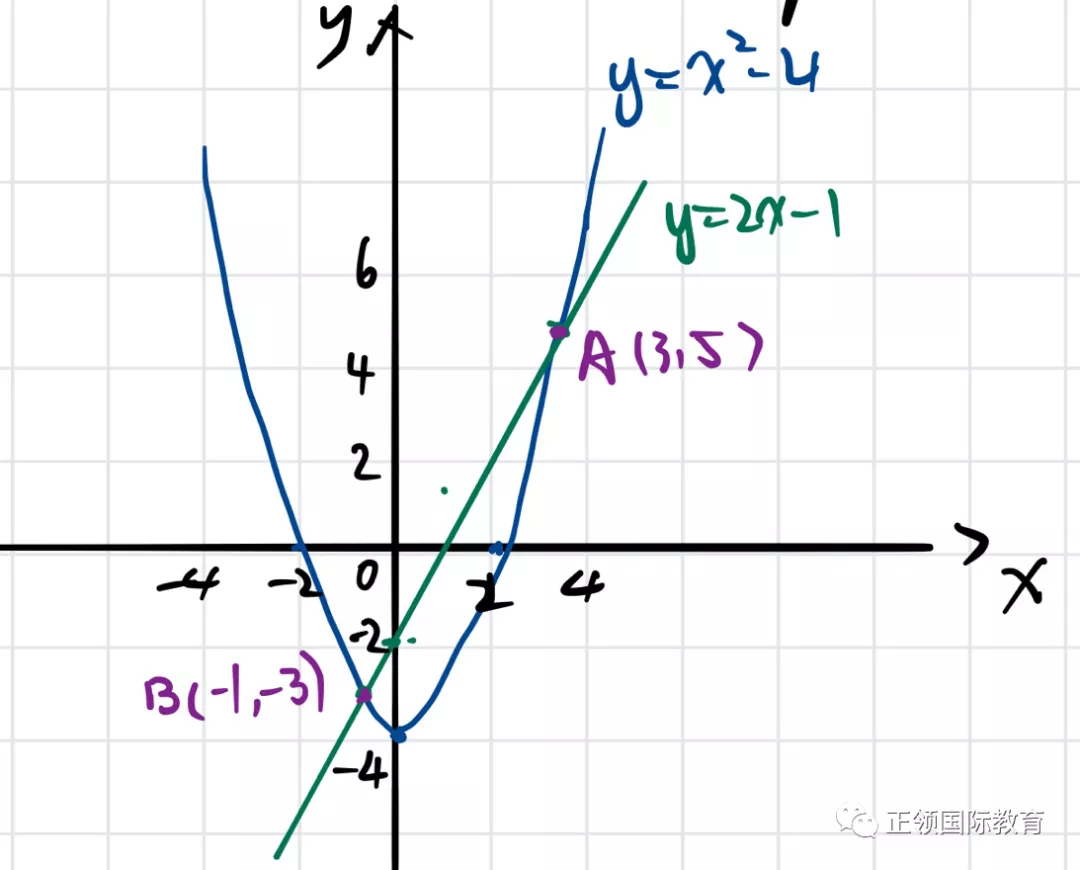
但我们也并不能每次都通过画图来得到答案，那通过代数的方法，具体该怎么解联立方程呢？