P1，M1，S1的真题都已经陆续给大家做了解析，今天终于轮到P3了，宝宝们有没有等的很心急呢~

让大家久等了，接下来就给大家带来2017年10月CIE真题纯数3第二套详解！

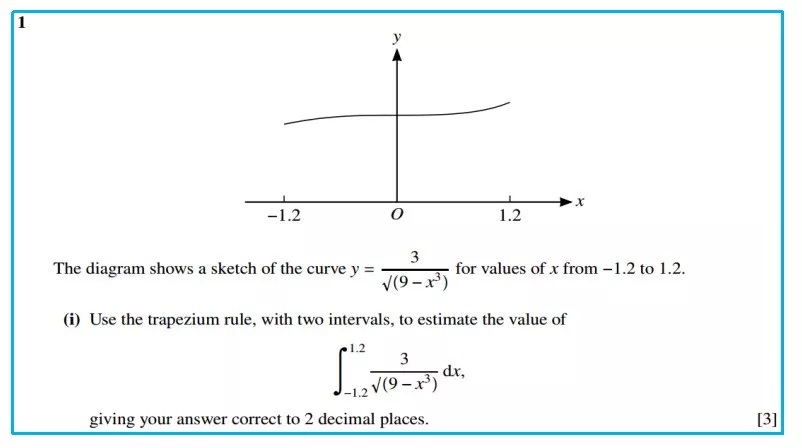
思路：把积分区间-1.2到1.2均分成两个小区间，计算3个分点及相应的函数值，代入公式：

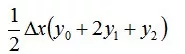
解答：

解答：It has both overestimation and underestimation.

思路：通过公式

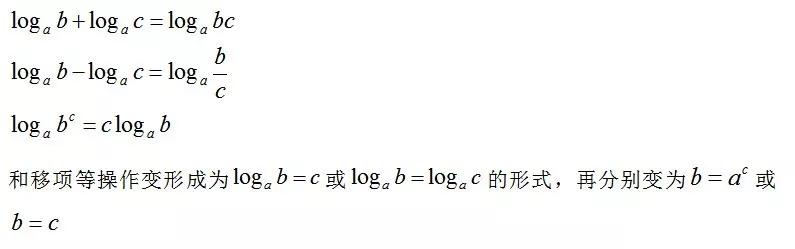
解答：

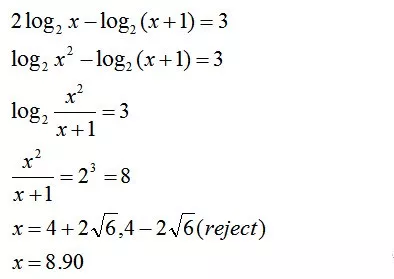
注：

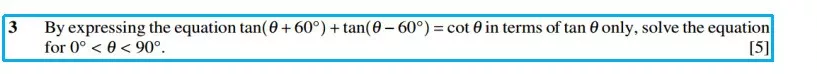
思路：

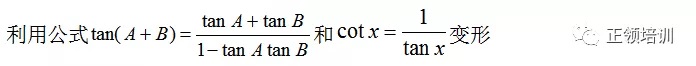
解答：

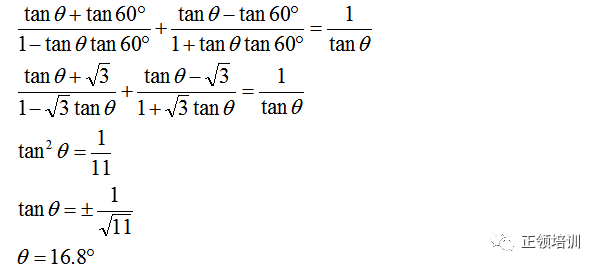
思路：令微分等于0，解出x和y

解答：

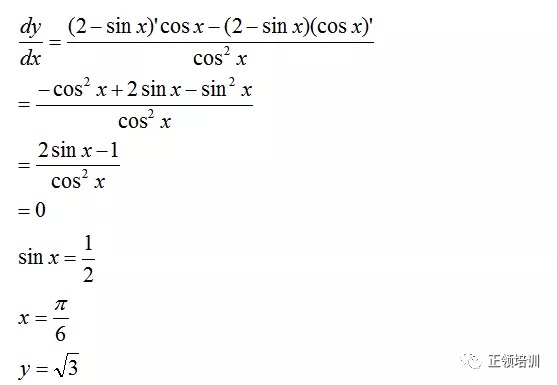
思路：把x代入二阶微分，大于0是minimum，小于0是maximum

解答：

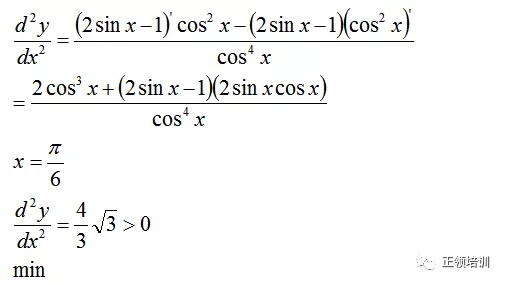
思路：把x和y分到等式两边，两边各自积分，代入初始条件解出C

解答：

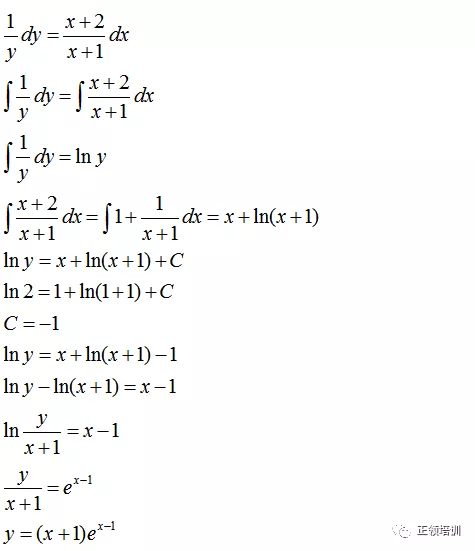
注：在解微分方程时，

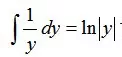
可以根据初始条件y=2判断绝对值内部为正，直接去掉绝对值

思路：等式两边同时微分，左边每项都是product rule

解答：

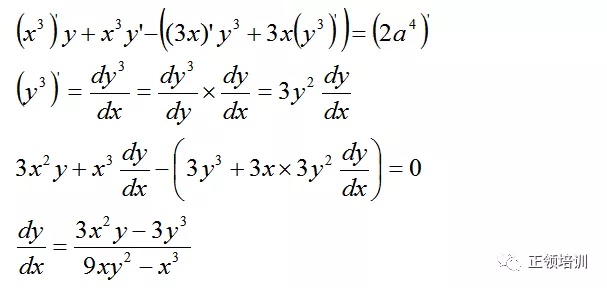
思路：

解答：

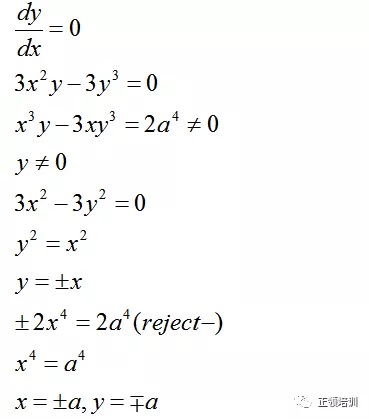
思路：

解答：

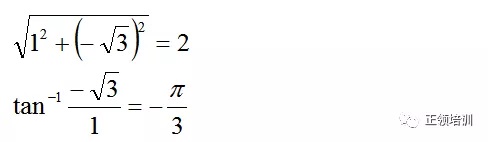
思路：直接代入计算，先算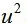

再乘以u得到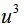

解答：

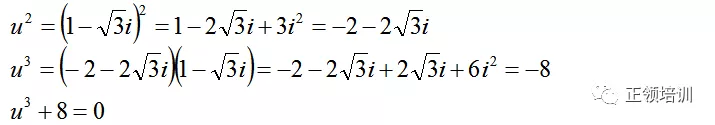
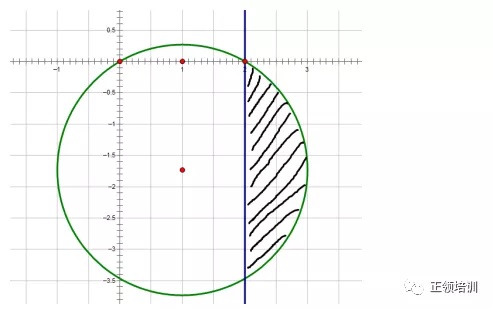
思路：argand diagram中，

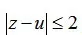
是以u为圆心，2为半径的圆的内部，

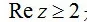
是横坐标大于等于2的区域，即直线x=2及其右边

解答：

思路：分子次数小于分母，直接拆

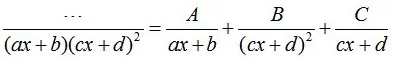
右边通分，令两边分子相等，代入特殊值或系数相等，算出A，B，C

解答：

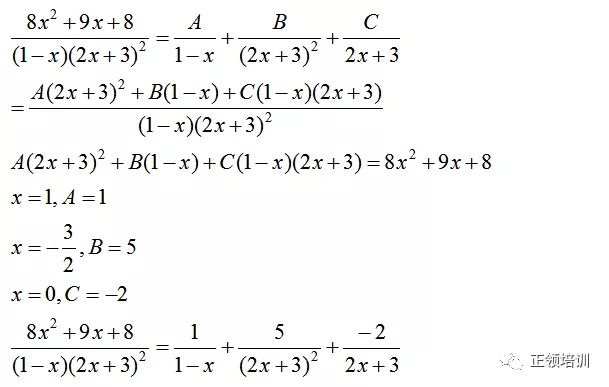
思路：把每一项写成

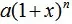
的形式，展开到2次项，再加起来

解答：

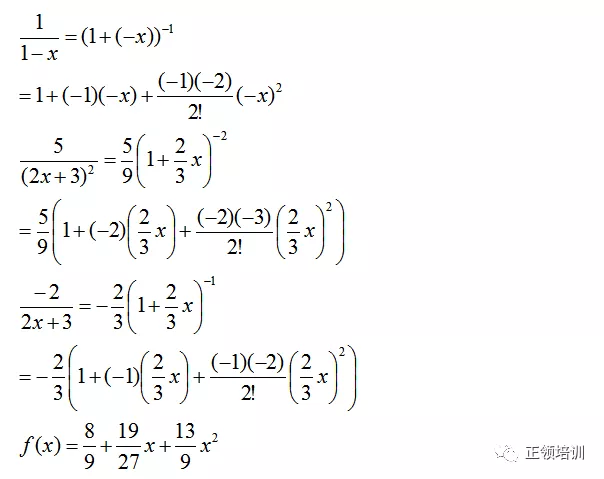
思路：用integration by parts计算积分，按照“指三幂对”的优先顺序挑选看作导数的函数

解答：

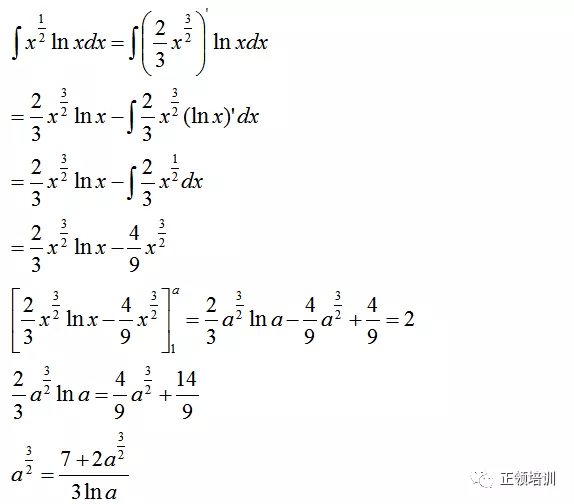
思路：证明某方程的根在a和b之间，把方程移项成f(x)=0的形式，验证f(a)和f(b)一正一负

解答：

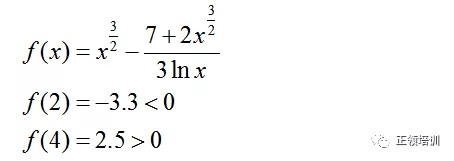
思路：利用计算器的ANS键直接计算，每次结果保留5位，当精确到3位不变时停止。题目没有给出初始值时，一般可取已知区间的中点作为初始值

解答：

思路：两平面所夹锐角，就是它们的法向量所夹锐角

解答：

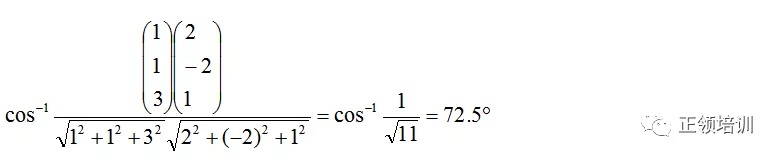
思路：把y=2代入p和q方程解出x和z可得A点坐标。所求平面同时垂直于另外两个平面，其法向量应该与另外两个平面的法向量都垂直，可用叉乘或方程组算出法向量，即为a,b,c，把A点坐标代入x,y,z可算出d

解答：

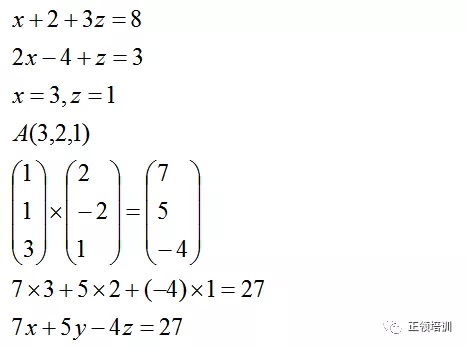
好了，今天的真题解析就讲到这儿了，接下来就看你们的了！